As seen in the picture
Zero is just a point in the world of numbers.
and also world of numbers is just a point in the world of infinity.
This lead us to think out of the box for what is beyond zero and infinity.
"Mathematics of Cyrene" is inspired by the ancient famous mathematicians "Eratosthenes of Cyrene" (276-194 BC), "Theodorus of Cyrene" (465-398 BC) and etc... This blog is about Advanced Mathematics topics, and my posts are reflecting my own point of view of many mathematical theories and problems, so that I may post some subjects that are not mentioned in literatures or mentioned in a different way. Mistakes could be happen as I learned math by my own way and thinking.
Tuesday, November 22, 2016
Monday, October 31, 2016
Theory of infinity
Soppose that:
$$y=\lim_{n \to +\infty} n$$
then $\frac 1y$ approaches $\frac 1{-y}$ as $n$ goes to $+\infty$
So, we can say that $\frac 1y \to \frac 1{-y}$
And therefore
$(y \to -y)$ as $(n \to +\infty)$
From this simple test we realize that there is only one infinity and the so-called $(+\infty , -\infty)$ are just two values approches to each other at one infinity without a sign ( without a sign because it is not a number)
So I can redefine the infinity as three types:
*Infinity: it is not a number therefore it has not a sign and it is equal to $\frac 10$
*Positive infinity: the biggest positive number and it is equal to $\frac 1{0^+}$
*Negative infinity: the smallest negative number and it is equal to $\frac 1{0^-}$
The methodology of this theory is like reimann sphere, but in this theory, I imagine the "numbers line" as very big circle that has diameter approaching to infinity so that its curve is really straight as we normally used to see it graphically.
One would say if $+\infty$ and $-\infty$ approaches to each other at infinity, why they give different values on a simple equation like $y=e^x$
$y=e^{+\infty}=+\infty$
$y=e^{-\infty}=0$
The answer of this question is quite simple.
because the same problem can happen to zero or any other number like this equation.
$y= \frac 1x$ has two different values at $x=0^+$ and $x=0^-$ and I can give many different example of two different limits around one number (left and right side).
So does it means we have two different zeros or numbers, absolutely not.
$$y=\lim_{n \to +\infty} n$$
then $\frac 1y$ approaches $\frac 1{-y}$ as $n$ goes to $+\infty$
So, we can say that $\frac 1y \to \frac 1{-y}$
And therefore
$(y \to -y)$ as $(n \to +\infty)$
From this simple test we realize that there is only one infinity and the so-called $(+\infty , -\infty)$ are just two values approches to each other at one infinity without a sign ( without a sign because it is not a number)
So I can redefine the infinity as three types:
*Infinity: it is not a number therefore it has not a sign and it is equal to $\frac 10$
*Positive infinity: the biggest positive number and it is equal to $\frac 1{0^+}$
*Negative infinity: the smallest negative number and it is equal to $\frac 1{0^-}$
The methodology of this theory is like reimann sphere, but in this theory, I imagine the "numbers line" as very big circle that has diameter approaching to infinity so that its curve is really straight as we normally used to see it graphically.
One would say if $+\infty$ and $-\infty$ approaches to each other at infinity, why they give different values on a simple equation like $y=e^x$
$y=e^{+\infty}=+\infty$
$y=e^{-\infty}=0$
The answer of this question is quite simple.
because the same problem can happen to zero or any other number like this equation.
$y= \frac 1x$ has two different values at $x=0^+$ and $x=0^-$ and I can give many different example of two different limits around one number (left and right side).
So does it means we have two different zeros or numbers, absolutely not.
Wednesday, October 26, 2016
Logic relations of Monomial symmetric polynomials
You can visit Symmetric polynomial webpage on this link
http://en.wikipedia.org/wiki/Symmetric_polynomial#Monomial_symmetric_polynomials
Monomial symmetric polynomials is nice notation for symmetric polynomials especially when the polynomial becomes so long expression like,
$M_{(1,2)}(a,b,c,d,e)=ab^2+ac^2+ad^2+ae^2+ba^2+bc^2+bd^2+be^2+ca^2+cb^2+cd^2+ce^2+da^2+db^2+dc^2+de^2+ea^2+eb^2+ec^2+ed^2$
In this post I will give nice logic relations of Monomial symmetric polynomials, which can help to solve polynomial equations like cubic and quadric equations.
Now check this logic relations
1) $(a^2+b^2)-(a+b)(a+b)+ab(a^0+b^0)=0$
2) $(a^3+b^3+c^3)-(a+b+c)(a^2+b^2+c^2)+(ab+bc+ca)(a+b+c)-abc(a^0+b^0+c^0)=0$
For the next relation I will use the notation of Monomial symmetric polynomials
3) $M_{(4)}(a,b,c,d) - M_{(1)}(a,b,c,d) \cdot M_{(3)}(a,b,c,d) + M_{(1,1)}(a,b,c,d) \cdot M_{(2)}(a,b,c,d) - M_{(1,1,1)}(a,b,c,d) \cdot M_{(1)}(a,b,c,d) + M_{(1,1,1,1)}(a,b,c,d) \cdot M_{(0)}(a,b,c,d)=0$
And for more general form for 4 variables $(a,b,c,d)$ we have,
$M_{(n)}(a,b,c,d) - M_{(m)}(a,b,c,d) \cdot M_{(n-m)}(a,b,c,d) + M_{(m,m)}(a,b,c,d) \cdot M_{(n-2m)}(a,b,c,d) - M_{(m,m,m)}(a,b,c,d) \cdot M_{(n-3m)}(a,b,c,d) + M_{(m,m,m,m)}(a,b,c,d) \cdot M_{(n-4m)}(a,b,c,d) =0 $
for $(n = 4m)$
Or
$M_{(n)}(a,b,c,d) - M_{(m)}(a,b,c,d) \cdot M_{(n-m)}(a,b,c,d) + M_{(m,m)}(a,b,c,d) \cdot M_{(n-2m)}(a,b,c,d) - M_{(m,m,m)}(a,b,c,d) \cdot M_{(n-3m)}(a,b,c,d) + M_{(n-3m,m,m,m)}(a,b,c,d) =0$
for $(n \gt 4m)$
If we want to generalize the formula for unknown number of variables $(a_1,a_2, \cdots , a_n)$
We should have new definition of extended Monomial symmetric polynomials.
Let us define $M_{(k)}^{(n)}(a_1,a_2,\cdots , a_n)$ as a Monomial symmetric polynomials that has $n$ number of $k$ powers for the given variables.
So I can say:
$$M_{(k)}^{(n)}(a_1,a_2,\cdots , a_n)=M_{(k,k, … k)}(a_1,a_2, \cdots , a_n)$$ $k$ is repeated $n$ times.
The new definition will help us to construct a formula to generalize a relation for unknown number of variables $(a_1,a_2, \cdots , a_n)$
So we have,
$$\sum_{m=0}^{n}\left( (M_{(n-m)}^{(j)}(a_1,a_2, \cdots , a_n))\cdot \sum_{1}^{n} a_k^{jm}\right)=0$$
$j \in \Bbb N$
http://en.wikipedia.org/wiki/Symmetric_polynomial#Monomial_symmetric_polynomials
Monomial symmetric polynomials is nice notation for symmetric polynomials especially when the polynomial becomes so long expression like,
$M_{(1,2)}(a,b,c,d,e)=ab^2+ac^2+ad^2+ae^2+ba^2+bc^2+bd^2+be^2+ca^2+cb^2+cd^2+ce^2+da^2+db^2+dc^2+de^2+ea^2+eb^2+ec^2+ed^2$
In this post I will give nice logic relations of Monomial symmetric polynomials, which can help to solve polynomial equations like cubic and quadric equations.
Now check this logic relations
1) $(a^2+b^2)-(a+b)(a+b)+ab(a^0+b^0)=0$
2) $(a^3+b^3+c^3)-(a+b+c)(a^2+b^2+c^2)+(ab+bc+ca)(a+b+c)-abc(a^0+b^0+c^0)=0$
For the next relation I will use the notation of Monomial symmetric polynomials
3) $M_{(4)}(a,b,c,d) - M_{(1)}(a,b,c,d) \cdot M_{(3)}(a,b,c,d) + M_{(1,1)}(a,b,c,d) \cdot M_{(2)}(a,b,c,d) - M_{(1,1,1)}(a,b,c,d) \cdot M_{(1)}(a,b,c,d) + M_{(1,1,1,1)}(a,b,c,d) \cdot M_{(0)}(a,b,c,d)=0$
And for more general form for 4 variables $(a,b,c,d)$ we have,
$M_{(n)}(a,b,c,d) - M_{(m)}(a,b,c,d) \cdot M_{(n-m)}(a,b,c,d) + M_{(m,m)}(a,b,c,d) \cdot M_{(n-2m)}(a,b,c,d) - M_{(m,m,m)}(a,b,c,d) \cdot M_{(n-3m)}(a,b,c,d) + M_{(m,m,m,m)}(a,b,c,d) \cdot M_{(n-4m)}(a,b,c,d) =0 $
for $(n = 4m)$
Or
$M_{(n)}(a,b,c,d) - M_{(m)}(a,b,c,d) \cdot M_{(n-m)}(a,b,c,d) + M_{(m,m)}(a,b,c,d) \cdot M_{(n-2m)}(a,b,c,d) - M_{(m,m,m)}(a,b,c,d) \cdot M_{(n-3m)}(a,b,c,d) + M_{(n-3m,m,m,m)}(a,b,c,d) =0$
for $(n \gt 4m)$
If we want to generalize the formula for unknown number of variables $(a_1,a_2, \cdots , a_n)$
We should have new definition of extended Monomial symmetric polynomials.
Let us define $M_{(k)}^{(n)}(a_1,a_2,\cdots , a_n)$ as a Monomial symmetric polynomials that has $n$ number of $k$ powers for the given variables.
So I can say:
$$M_{(k)}^{(n)}(a_1,a_2,\cdots , a_n)=M_{(k,k, … k)}(a_1,a_2, \cdots , a_n)$$ $k$ is repeated $n$ times.
The new definition will help us to construct a formula to generalize a relation for unknown number of variables $(a_1,a_2, \cdots , a_n)$
So we have,
$$\sum_{m=0}^{n}\left( (M_{(n-m)}^{(j)}(a_1,a_2, \cdots , a_n))\cdot \sum_{1}^{n} a_k^{jm}\right)=0$$
$j \in \Bbb N$
Tuesday, October 18, 2016
Unified method to find formula for polynomial equation roots.
Here is unified solution routine to find formula for any $nth$ degree equation , for $n < 5$
We can write The general form for any polynomial equation of any $nth$ degree as:
$$\sum_{j=0}^{n} a_j x^j =a_0+a_1x+a_2x^2+\cdots + a_nx^n =0$$
where $a_n \neq 0$
After dividing the equation by $a_n$ , the substitution $x=y-\frac{a_{n-1}}{na_n}$ will eliminate the term $a_{n-1}x^{n-1}$ so we have,
$$\sum_{j=0}^{n}\left(b_jy^j\right) -b_{n-1}y^{n-1}=b_0+b_1y+b_2y^2+\cdots+b_{n-2}y^{n-2}+b_ny^n$$
As we know that the quadratic equation is already solved by this substitution , but remain the cubic and the quartic which will be solved in the following steps:
For the cubic equation, I will rewrite it as,
$$y^3+py+q=0 \tag1$$
Let $y=z_1+z_2$
$y^3=z_1^3+3z_1^2z_2+3z_1z_2^2+z_2^3=z_1^3+3z_1z_2(z_1+z_2)+z_2^3$
$$y^3-3z_1z_2x-(z_1^3+z_2^3)=0 \tag 2$$
By comparing the coefficients of $eq(2)$ with the original equation (1) we get,
$p=-3z_1z_2 \Rightarrow z_1^3z_2^3=\frac{-p^3}{27}$
and
$q=-(z_1^3+z_2^3)$
assume that $z_1^3$ and $z_2^3$ are roots of $z^3$ then we can write the equation as,
$$(z^3-z_1^3)(z^3-z_2^3)=0$$
and by expanding the equation we have,
$$z^6-(z_1^3+z_2^3)z^3+z_1^3z_2^3=0$$
So we finally have,
$$z^6+qz^3-\frac{p^3}{27}=0$$
$z_1=\sqrt[3]{-\frac q2+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$
$z_2=\sqrt[3]{-\frac q2-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$
$$\begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ \end{bmatrix}=\begin{bmatrix} z_1 \\ z_2 \\ \end{bmatrix} * \begin{bmatrix} 1 & 1 \\ \omega & \omega^2 \\ \omega^2 & \omega \\ \end{bmatrix}$$
$\omega$ is imaginary cubic root of unity.
$x_j=y_j-\frac{a_2}{3a_3} , j=1,2,3$
For the quartic equation, I will rewrite it as,
$$y^4+py^2+qy+r=0 \tag 3$$
Let $y=z_1+z_2+z_3$
By squaring both sides
$y^2=z_1^2+z_2^2+z_3^2+2(z_1 z_2+z_1 z_3+z_2 z_3)$
$y^2-(z_1^2+z_2^2+z_3^2)=2(z_1 z_2+z_1 z_3+z_2 z_3)$
By squaring both sides again.
$y^4-2(z_1^2+z_2^2+z_3^2 ) y^2+(z_1^2+z_2^2+z_3^2 )^2=4(z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2+2(z_1^2 z_2 z_3+z_1 z_2^2 z_3+z_1 z_2 z_3^2 ))$
$y^4-2(z_1^2+z_2^2+z_3^2 ) y^2+(z_1^2+z_2^2+z_3^2 )^2=4(z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2)+8z_1 z_2 z_3 (z_1+z_2+z_3 )$
$$y^4-2(z_1^2+z_2^2+z_3^2 ) y^2-8(z_1 z_2 z_3)y+(z_1^2+z_2^2+z_3^2 )^2-4(z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2 )=0 \tag 4$$
By comparing the coefficients of $eq(4)$ with the original equation (3) we get,
$p=-2(z_1^2+z_2^2+z_3^2 )$
$q=-8(z_1 z_2 z_3 )$
$r=(z_1^2+z_2^2+z_3^2 )^2-4(z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2 )$
and by some little steps of substitution we get,
$z_1^2+z_2^2+z_3^2 =-\frac p2$
$z_1^2 z_2^2 z_3^2=\frac {q^2}{64}$
$z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2=\frac{p^2-4r}{16}$
assume that $z_1^2$ , $z_2^2$ and $z_3^2$ are roots of $z^2$ then we can write the equation as,
$$(z^2-z_1^2)(z^2-z_2^2)(z^2-z_3^2)=0$$
and by expanding the equation we have,
$$z^6-(z_1^2+z_2^2+z_3^2 ) z^4+(z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2 ) z^2-z_1^2 z_2^2 z_3^2=0$$
By substitution we get a cubic equation,
$$z^6+\frac p2 z^4+\left(\frac{p^2-4r}{16}\right) z^2-\frac{q^2}{64}=0$$
So we finally have,
$$\begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ \end{bmatrix}=\begin{bmatrix} z_1 \\ z_2 \\ z_3 \\ \end{bmatrix} * \begin{bmatrix} 1 & 1 & 1 \\ 1 & -1 & -1 \\ -1 & 1 & -1 \\ -1 & -1& 1 \\ \end{bmatrix}$$
$x_j=y_j-\frac{a_3}{4a_4} , j= 1,2,3,4$
For higher degree equations,
There is no formula for higher degree equations in radicals
Abel–Ruffini theorem and Galois theory have proved the impossibility of solving quintic and higher degree equations in radicals.
We can write The general form for any polynomial equation of any $nth$ degree as:
$$\sum_{j=0}^{n} a_j x^j =a_0+a_1x+a_2x^2+\cdots + a_nx^n =0$$
where $a_n \neq 0$
After dividing the equation by $a_n$ , the substitution $x=y-\frac{a_{n-1}}{na_n}$ will eliminate the term $a_{n-1}x^{n-1}$ so we have,
$$\sum_{j=0}^{n}\left(b_jy^j\right) -b_{n-1}y^{n-1}=b_0+b_1y+b_2y^2+\cdots+b_{n-2}y^{n-2}+b_ny^n$$
As we know that the quadratic equation is already solved by this substitution , but remain the cubic and the quartic which will be solved in the following steps:
For the cubic equation, I will rewrite it as,
$$y^3+py+q=0 \tag1$$
Let $y=z_1+z_2$
$y^3=z_1^3+3z_1^2z_2+3z_1z_2^2+z_2^3=z_1^3+3z_1z_2(z_1+z_2)+z_2^3$
$$y^3-3z_1z_2x-(z_1^3+z_2^3)=0 \tag 2$$
By comparing the coefficients of $eq(2)$ with the original equation (1) we get,
$p=-3z_1z_2 \Rightarrow z_1^3z_2^3=\frac{-p^3}{27}$
and
$q=-(z_1^3+z_2^3)$
assume that $z_1^3$ and $z_2^3$ are roots of $z^3$ then we can write the equation as,
$$(z^3-z_1^3)(z^3-z_2^3)=0$$
and by expanding the equation we have,
$$z^6-(z_1^3+z_2^3)z^3+z_1^3z_2^3=0$$
So we finally have,
$$z^6+qz^3-\frac{p^3}{27}=0$$
$z_1=\sqrt[3]{-\frac q2+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$
$z_2=\sqrt[3]{-\frac q2-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$
$$\begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ \end{bmatrix}=\begin{bmatrix} z_1 \\ z_2 \\ \end{bmatrix} * \begin{bmatrix} 1 & 1 \\ \omega & \omega^2 \\ \omega^2 & \omega \\ \end{bmatrix}$$
$\omega$ is imaginary cubic root of unity.
$x_j=y_j-\frac{a_2}{3a_3} , j=1,2,3$
For the quartic equation, I will rewrite it as,
$$y^4+py^2+qy+r=0 \tag 3$$
Let $y=z_1+z_2+z_3$
By squaring both sides
$y^2=z_1^2+z_2^2+z_3^2+2(z_1 z_2+z_1 z_3+z_2 z_3)$
$y^2-(z_1^2+z_2^2+z_3^2)=2(z_1 z_2+z_1 z_3+z_2 z_3)$
By squaring both sides again.
$y^4-2(z_1^2+z_2^2+z_3^2 ) y^2+(z_1^2+z_2^2+z_3^2 )^2=4(z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2+2(z_1^2 z_2 z_3+z_1 z_2^2 z_3+z_1 z_2 z_3^2 ))$
$y^4-2(z_1^2+z_2^2+z_3^2 ) y^2+(z_1^2+z_2^2+z_3^2 )^2=4(z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2)+8z_1 z_2 z_3 (z_1+z_2+z_3 )$
$$y^4-2(z_1^2+z_2^2+z_3^2 ) y^2-8(z_1 z_2 z_3)y+(z_1^2+z_2^2+z_3^2 )^2-4(z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2 )=0 \tag 4$$
By comparing the coefficients of $eq(4)$ with the original equation (3) we get,
$p=-2(z_1^2+z_2^2+z_3^2 )$
$q=-8(z_1 z_2 z_3 )$
$r=(z_1^2+z_2^2+z_3^2 )^2-4(z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2 )$
and by some little steps of substitution we get,
$z_1^2+z_2^2+z_3^2 =-\frac p2$
$z_1^2 z_2^2 z_3^2=\frac {q^2}{64}$
$z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2=\frac{p^2-4r}{16}$
assume that $z_1^2$ , $z_2^2$ and $z_3^2$ are roots of $z^2$ then we can write the equation as,
$$(z^2-z_1^2)(z^2-z_2^2)(z^2-z_3^2)=0$$
and by expanding the equation we have,
$$z^6-(z_1^2+z_2^2+z_3^2 ) z^4+(z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2 ) z^2-z_1^2 z_2^2 z_3^2=0$$
By substitution we get a cubic equation,
$$z^6+\frac p2 z^4+\left(\frac{p^2-4r}{16}\right) z^2-\frac{q^2}{64}=0$$
So we finally have,
$$\begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ \end{bmatrix}=\begin{bmatrix} z_1 \\ z_2 \\ z_3 \\ \end{bmatrix} * \begin{bmatrix} 1 & 1 & 1 \\ 1 & -1 & -1 \\ -1 & 1 & -1 \\ -1 & -1& 1 \\ \end{bmatrix}$$
$x_j=y_j-\frac{a_3}{4a_4} , j= 1,2,3,4$
For higher degree equations,
There is no formula for higher degree equations in radicals
Abel–Ruffini theorem and Galois theory have proved the impossibility of solving quintic and higher degree equations in radicals.
Friday, October 14, 2016
A study on half-order differentiation of exponential function
Before you read this topic I advise you to read the following posts first.
The Binomial Theorem proof by exponentials
Fractional Calculus of Zero
Disproving D^{1/2}e^x=e^x with explanation
The following picture is showing graphically the relation between $e^x$ expansion terms and Reciprocal gamma function.
The plot is for $x=1,x=2,x=3$
Also it shows the differentiation and integration manner of $e^x$.
So if we move the terms of $e^x$ half step to the direction of differentiation, we will get the terms of half-integers order differentiation.
$$D_x^{1/2}(e^x)=\cdots +\frac{x^{-3/2}}{(-3/2)!}+\frac{x^{-1/2}}{(-1/2)!}+\frac{x^{1/2}}{(1/2)!}+\frac{x^{3/2}}{(3/2)!}+\cdots$$
(Note that when I use non-integer factorials (a)! I am indeed referring to Gamma function)
Now the question which I am trying to answer is:
"Does this series converges? and how to deal with it in case of it diverges?"
I will use $e_{\alpha}^x$ as annotation for $D_x^{\alpha}(e^x)$
I recently proved this nice relation where $a,b \in \Bbb R$
$$e^a\cdot e_{\alpha}^b=e_{\alpha}^{a+b} \tag1$$
Which I can prove it by using the binomial formula from the previous post
$$\frac{(a+b)^{\alpha}}{\alpha!}=\sum_{k \in \Bbb Z} \frac{a^k}{k!} \cdot \frac{b^{\alpha-k}}{(\alpha-k)!}$$
And I already proved ,in the previous post, that the binomial theorem is actually a term of two multiplied exponential function ($\alpha$ can be any real number).
By using $eq(1)$ let us now test the relation for $\alpha=\frac12$
For $a=0$ we have,
$e^0\cdot e_{1/2}^b=e_{1/2}^{0+b} \Rightarrow e_{1/2}^b=e_{1/2}^b$
and that is a logical result.
For $b=0$ we have,
$e^a\cdot e_{1/2}^0=e_{1/2}^{a+0} \Rightarrow e^a \cdot e_{1/2}^0=e_{1/2}^a$
We all know that $e_{1/2}^0=\infty$
Hence $$e_{1/2}^a=\infty \cdot e^a$$
Therefore the expansion series of $e_{1/2}^a$ is not well-defined, but actually if we look to fractional calculus of 'zero number' which I studied it before in an earlier post makes the whole fractional calculus undefined and for that reason we always set the zero fractional calculus value to zero.
Thus we always have to eliminate the expansion series terms of $e_{1/2}^a$ that met the half-order differentiation of zero expansion so that it finally converges.
$$D_x^{1/2}(e^x)=\frac{x^{-1/2}}{(-1/2)!}+\frac{x^{1/2}}{(1/2)!}+\frac{x^{3/2}}{(3/2)!}+\frac{x^{5/2}}{(5/2)!}+\cdots$$
The Binomial Theorem proof by exponentials
Fractional Calculus of Zero
Disproving D^{1/2}e^x=e^x with explanation
The following picture is showing graphically the relation between $e^x$ expansion terms and Reciprocal gamma function.
The plot is for $x=1,x=2,x=3$
Also it shows the differentiation and integration manner of $e^x$.
Click on the image to enlarge it
So if we move the terms of $e^x$ half step to the direction of differentiation, we will get the terms of half-integers order differentiation.
$$D_x^{1/2}(e^x)=\cdots +\frac{x^{-3/2}}{(-3/2)!}+\frac{x^{-1/2}}{(-1/2)!}+\frac{x^{1/2}}{(1/2)!}+\frac{x^{3/2}}{(3/2)!}+\cdots$$
(Note that when I use non-integer factorials (a)! I am indeed referring to Gamma function)
Now the question which I am trying to answer is:
"Does this series converges? and how to deal with it in case of it diverges?"
I will use $e_{\alpha}^x$ as annotation for $D_x^{\alpha}(e^x)$
I recently proved this nice relation where $a,b \in \Bbb R$
$$e^a\cdot e_{\alpha}^b=e_{\alpha}^{a+b} \tag1$$
Which I can prove it by using the binomial formula from the previous post
$$\frac{(a+b)^{\alpha}}{\alpha!}=\sum_{k \in \Bbb Z} \frac{a^k}{k!} \cdot \frac{b^{\alpha-k}}{(\alpha-k)!}$$
And I already proved ,in the previous post, that the binomial theorem is actually a term of two multiplied exponential function ($\alpha$ can be any real number).
By using $eq(1)$ let us now test the relation for $\alpha=\frac12$
For $a=0$ we have,
$e^0\cdot e_{1/2}^b=e_{1/2}^{0+b} \Rightarrow e_{1/2}^b=e_{1/2}^b$
and that is a logical result.
For $b=0$ we have,
$e^a\cdot e_{1/2}^0=e_{1/2}^{a+0} \Rightarrow e^a \cdot e_{1/2}^0=e_{1/2}^a$
We all know that $e_{1/2}^0=\infty$
Hence $$e_{1/2}^a=\infty \cdot e^a$$
Therefore the expansion series of $e_{1/2}^a$ is not well-defined, but actually if we look to fractional calculus of 'zero number' which I studied it before in an earlier post makes the whole fractional calculus undefined and for that reason we always set the zero fractional calculus value to zero.
Thus we always have to eliminate the expansion series terms of $e_{1/2}^a$ that met the half-order differentiation of zero expansion so that it finally converges.
$$D_x^{1/2}(e^x)=\frac{x^{-1/2}}{(-1/2)!}+\frac{x^{1/2}}{(1/2)!}+\frac{x^{3/2}}{(3/2)!}+\frac{x^{5/2}}{(5/2)!}+\cdots$$
Friday, September 30, 2016
The Binomial Theorem proof by exponentials.
The famous furmula for the binomial is
$$(a+b)^n=\sum_{k=0}^{\infty} \binom nk a^k b^{n-k}$$
But we can also express the formula like this
$${(a+b)^n \over n!}=\sum_{k \in \Bbb Z} \frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!}$$
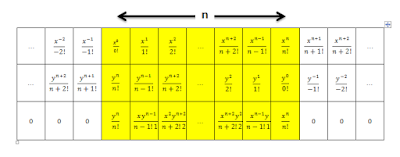
Actually the binomial structure is coming from the $nth$ term when multiplying two exponentials together , see the following picture.
The first row of the table is $e^x$ terms, the second row is $e^y$ terms arranged backwards and the last row is the result of multiplying every term from the first row by the opposite term in the second row.
The distance $n$ is from the zero term of the first row $e^x$ to the zero term of the second row $e^y$
So we can prove the binomial theorem by the following steps:
$$e^{a+b}=e^a e^b \tag1$$
$$\sum_{n \in \Bbb Z} \frac {(a+b)^n}{n!}=\left(\sum_{n \in \Bbb Z} \frac {a^n}{n!} \right) \left( \sum_{n \in \Bbb Z} \frac {b^n}{n!}\right) \tag2$$
We can use "Cauchy product of two infinite series" to multiply the two series in RHS in $eq(2)$.
$$\left(\sum_{n \in \Bbb Z} \frac {a^n}{n!} \right) \left( \sum_{n \in \Bbb Z} \frac {b^n}{n!}\right)=\sum_{n \in \Bbb Z}\left( \sum_{k \in \Bbb Z}\frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!} \right) \tag3$$
From $eq(2)$ & $eq(3)$ we get:
$$\sum_{n \in \Bbb Z} \frac {(a+b)^n}{n!}=\sum_{n \in \Bbb Z}\left( \sum_{k \in \Bbb Z}\frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!} \right) \tag4$$
Now it is clearly that every term of the series in the LHS is equal to the same $nth$ term in the RHS.
So we finally have
$${(a+b)^n \over n!}=\sum_{k \in \Bbb Z} \frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!} \tag5$$
Which indeed the same known binomial formula:
$$(a+b)^n=\sum_{k=0}^{\infty} \binom nk a^k b^{n-k}$$
$$(a+b)^n=\sum_{k=0}^{\infty} \binom nk a^k b^{n-k}$$
But we can also express the formula like this
$${(a+b)^n \over n!}=\sum_{k \in \Bbb Z} \frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!}$$
Actually the binomial structure is coming from the $nth$ term when multiplying two exponentials together , see the following picture.
Click on the image to enlarge it
The first row of the table is $e^x$ terms, the second row is $e^y$ terms arranged backwards and the last row is the result of multiplying every term from the first row by the opposite term in the second row.
The distance $n$ is from the zero term of the first row $e^x$ to the zero term of the second row $e^y$
So we can prove the binomial theorem by the following steps:
$$e^{a+b}=e^a e^b \tag1$$
$$\sum_{n \in \Bbb Z} \frac {(a+b)^n}{n!}=\left(\sum_{n \in \Bbb Z} \frac {a^n}{n!} \right) \left( \sum_{n \in \Bbb Z} \frac {b^n}{n!}\right) \tag2$$
We can use "Cauchy product of two infinite series" to multiply the two series in RHS in $eq(2)$.
$$\left(\sum_{n \in \Bbb Z} \frac {a^n}{n!} \right) \left( \sum_{n \in \Bbb Z} \frac {b^n}{n!}\right)=\sum_{n \in \Bbb Z}\left( \sum_{k \in \Bbb Z}\frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!} \right) \tag3$$
From $eq(2)$ & $eq(3)$ we get:
$$\sum_{n \in \Bbb Z} \frac {(a+b)^n}{n!}=\sum_{n \in \Bbb Z}\left( \sum_{k \in \Bbb Z}\frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!} \right) \tag4$$
Now it is clearly that every term of the series in the LHS is equal to the same $nth$ term in the RHS.
So we finally have
$${(a+b)^n \over n!}=\sum_{k \in \Bbb Z} \frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!} \tag5$$
Which indeed the same known binomial formula:
$$(a+b)^n=\sum_{k=0}^{\infty} \binom nk a^k b^{n-k}$$
Saturday, September 24, 2016
Disproving of $\frac{d^{1/2}}{dx^{1/2}}e^x = e^x$ with explanation.
Its clear that the devirative of $e^x$ equal itself for the integer order differentiation.
So does it means that it is allowed to equal itself for the half order as well?
Have you asked yourself if there is a function equal itself only every $even$ order or every $nth$ order throughout its multiples?
See the behavior of the following functions where $n \in \Bbb Z$
1) $D^{n}_x( e^x)=e^x $ (neutral function of integer-order Diffrentiation)
2) $D^{2n}_x\left(\frac{e^x+e^{-x}}{2}\right )=\frac{e^x+e^{-x}}{2}$ (neutral function of only even-order Diffrentiation)
3) $D^{3n}_x\left(\frac {e^x+e^{\omega x}+e^{\omega^2 x}}{3}\right)=\frac {e^x+e^{\omega x}+e^{\omega^2 x}}{3}$ where $\omega=e^{\frac{\pi i}{3}}$ (neutral function of only multiples-of-3-order Diffrentiation)
4) $D^{4n}_x\left(\frac {e^x+e^{-x}+e^{ix}+e^{-ix}}{4}\right)=\frac {e^x+e^{-x}+e^{ix}+e^{-ix}}{4}$ (neutral function of only multiples-of-4-order Diffrentiation)
and so on...
These belong to exponential k step $\sum_{k \in \Bbb Z}\frac{x^{nk}}{(nk)!}$ any every function of them can not equal itself with an order out of its $nth$ order and its multiples.
(Exponential k step has a formula for generating any k step , $\sum_{k \in \Bbb Z}\frac{x^{nk}}{(nk)!}=\frac1k\sum_{j=1}^{k}e^{r^j_k x}$ where $r_k=e^{\frac{2\pi i}{k}}$)
Now let us rearrange the functions in other patern.
In the following steps I will use Mittag-Leffler function instead of k step sum but with little change as:
$$E_{\alpha}(x^{\alpha})=\sum_{k \in \Bbb Z}\frac{x^{\alpha k}}{(\alpha k)!} , \alpha >0 \tag 1$$
1) For $\alpha=1$ , $E_{1}(x)=e^x$
2) For $\alpha =2$ , $E_{2}(x^2)=\frac12(e^x+e^{-x})$
3) For $\alpha =4$ , $E_{4}(x^4)=\frac14(e^x+e^{-x}+e^{ix}+e^{-ix})$
4) For $\alpha =8$ , $E_{8}(x^8)=\frac18(e^x+e^{-x}+e^{ix}+e^{-ix}+e^{(i+1)x}+e^{(i-1)x}+e^{(-i+1)x}+e^{(-i-1)x})$
and so on every $2^n$ itration
We can obseve two relations
$$E_{2\alpha}(x^{2\alpha})=\frac12\left(E_{\alpha}(x^{\alpha})+E_{\alpha}\left((-1)^{\frac1{\alpha}}x^{\alpha}\right)\right) \tag 2$$
and
$$E_{\alpha}(x^{\alpha})=E_{2\alpha}(x^{2\alpha})+D_x^{\alpha}\left(E_{2\alpha}(x^{2\alpha})\right) \tag 3$$
For example:
$E_1(x)=E_2(x^2)+D^1_x(E_2(x^2))$
$=\frac12(e^x+e^{-x})+D^1_x\left(\frac12(e^x+e^{-x})\right)$
$=\frac12(e^x+e^{-x})+\frac12(e^x-e^{-x})=e^x$
Now if we let $\alpha = \frac12$ then
$E_{1/2}(x^{1/2})=E_1(x)+D_x^{1/2}(E_1(x))$
$=e^x+D_x^{1/2}(e^x)$
From eq(1) we have $$E_{1/2}(x^{1/2})=\sum_{k \in \Bbb Z}\frac{x^{\frac12 k}}{(\frac12 k)!}=\cdots +\frac{x^{-1}}{-1!}+\frac{x^{-1/2}}{-1/2!}+\frac{x^0}{0!}+\frac{x^{1/2}}{1/2!}+\frac{x^1}{1!}+\frac{x^{3/2}}{3/2!}+\frac{x^2}{2!}+\frac{x^{5/2}}{5/2!}+\cdots$$
Then
$$e^x+D_x^{1/2}(e^x)=\left(\cdots +\frac{x^{-1}}{-1!}+\frac{x^0}{0!}+\frac{x}{1!}+\frac{x^2}{2!}+\cdots\right)+\left(\cdots +\frac{x^{-1/2}}{-1/2!}+\frac{x^{1/2}}{1/2!}+\frac{x^{3/2}}{3/2!}+\frac{x^{5/2}}{5/2!}+\cdots\right)$$
Therefore
$$D_x^{1/2}(e^x)=\cdots +\frac{x^{-5/2}}{-5/2!}+\frac{x^{-3/2}}{-3/2!}+\frac{x^{-1/2}}{-1/2!}+\frac{x^{1/2}}{1/2!}+\frac{x^{3/2}}{3/2!}+\frac{x^{5/2}}{5/2!}+\cdots$$
Unfortunately the half-order differentiation of $e^x$ is undefined by this series expansion.
AN OTHER PROOF
Let us assume that $D_x^{1/2}(e^{ax})=a^{1/2}e^{ax}$ that means:
$$D_x^{1/2}\left(\lim_{n \to \infty}(1+\frac1n)^{n(ax)}\right)=a^{1/2}\left(\lim_{n \to \infty}(1+\frac1n)^{n(ax)}\right)$$
And also by exponential property it can be written as:
$$D_x^{1/2}\left(\lim_{n \to \infty}(1+\frac anx)^{n}\right)=a^{1/2}\left(\lim_{n \to \infty}(1+\frac anx)^{n}\right)$$
Now the equation is under power role which seems to be ok for any integer-order differentioation.
Because $n$ is constant so it can be any positive real vlaue, and we expect the same result for any value of $n$.
Then for the first test $(n=1)$,
$$D_x^{1/2}\left((1+ ax)^{(1)}\right)=\frac{a^{1/2}}{\Gamma(3/2)}(1+ax)^{(\frac12)}$$
But if we solve it directly we get,
$$D_x^{1/2}\left(1+ ax\right)=\frac{x^{-1/2}}{\Gamma(1/2)}+a\frac{x^{1/2}}{\Gamma(3/2)}$$
And we can simply see that,
$$\frac{a^{1/2}}{\Gamma(3/2)}(1+ax)^{(\frac12)} \neq \frac{x^{-1/2}}{\Gamma(1/2)}+a\frac{x^{1/2}}{\Gamma(3/2)}$$
Hence the first test $"n=1"$ has failed.
FINALLY
Nevertheless there is a relation which says
$$D_x^{\alpha}(e^x)=e^x \cdot D_x^{\alpha}(e^x)|_{x=0}$$
Which I will prove it in one of the next posts (If God wills).
So does it means that it is allowed to equal itself for the half order as well?
Have you asked yourself if there is a function equal itself only every $even$ order or every $nth$ order throughout its multiples?
See the behavior of the following functions where $n \in \Bbb Z$
1) $D^{n}_x( e^x)=e^x $ (neutral function of integer-order Diffrentiation)
2) $D^{2n}_x\left(\frac{e^x+e^{-x}}{2}\right )=\frac{e^x+e^{-x}}{2}$ (neutral function of only even-order Diffrentiation)
3) $D^{3n}_x\left(\frac {e^x+e^{\omega x}+e^{\omega^2 x}}{3}\right)=\frac {e^x+e^{\omega x}+e^{\omega^2 x}}{3}$ where $\omega=e^{\frac{\pi i}{3}}$ (neutral function of only multiples-of-3-order Diffrentiation)
4) $D^{4n}_x\left(\frac {e^x+e^{-x}+e^{ix}+e^{-ix}}{4}\right)=\frac {e^x+e^{-x}+e^{ix}+e^{-ix}}{4}$ (neutral function of only multiples-of-4-order Diffrentiation)
and so on...
These belong to exponential k step $\sum_{k \in \Bbb Z}\frac{x^{nk}}{(nk)!}$ any every function of them can not equal itself with an order out of its $nth$ order and its multiples.
(Exponential k step has a formula for generating any k step , $\sum_{k \in \Bbb Z}\frac{x^{nk}}{(nk)!}=\frac1k\sum_{j=1}^{k}e^{r^j_k x}$ where $r_k=e^{\frac{2\pi i}{k}}$)
Now let us rearrange the functions in other patern.
In the following steps I will use Mittag-Leffler function instead of k step sum but with little change as:
$$E_{\alpha}(x^{\alpha})=\sum_{k \in \Bbb Z}\frac{x^{\alpha k}}{(\alpha k)!} , \alpha >0 \tag 1$$
1) For $\alpha=1$ , $E_{1}(x)=e^x$
2) For $\alpha =2$ , $E_{2}(x^2)=\frac12(e^x+e^{-x})$
3) For $\alpha =4$ , $E_{4}(x^4)=\frac14(e^x+e^{-x}+e^{ix}+e^{-ix})$
4) For $\alpha =8$ , $E_{8}(x^8)=\frac18(e^x+e^{-x}+e^{ix}+e^{-ix}+e^{(i+1)x}+e^{(i-1)x}+e^{(-i+1)x}+e^{(-i-1)x})$
and so on every $2^n$ itration
We can obseve two relations
$$E_{2\alpha}(x^{2\alpha})=\frac12\left(E_{\alpha}(x^{\alpha})+E_{\alpha}\left((-1)^{\frac1{\alpha}}x^{\alpha}\right)\right) \tag 2$$
and
$$E_{\alpha}(x^{\alpha})=E_{2\alpha}(x^{2\alpha})+D_x^{\alpha}\left(E_{2\alpha}(x^{2\alpha})\right) \tag 3$$
For example:
$E_1(x)=E_2(x^2)+D^1_x(E_2(x^2))$
$=\frac12(e^x+e^{-x})+D^1_x\left(\frac12(e^x+e^{-x})\right)$
$=\frac12(e^x+e^{-x})+\frac12(e^x-e^{-x})=e^x$
Now if we let $\alpha = \frac12$ then
$E_{1/2}(x^{1/2})=E_1(x)+D_x^{1/2}(E_1(x))$
$=e^x+D_x^{1/2}(e^x)$
From eq(1) we have $$E_{1/2}(x^{1/2})=\sum_{k \in \Bbb Z}\frac{x^{\frac12 k}}{(\frac12 k)!}=\cdots +\frac{x^{-1}}{-1!}+\frac{x^{-1/2}}{-1/2!}+\frac{x^0}{0!}+\frac{x^{1/2}}{1/2!}+\frac{x^1}{1!}+\frac{x^{3/2}}{3/2!}+\frac{x^2}{2!}+\frac{x^{5/2}}{5/2!}+\cdots$$
Then
$$e^x+D_x^{1/2}(e^x)=\left(\cdots +\frac{x^{-1}}{-1!}+\frac{x^0}{0!}+\frac{x}{1!}+\frac{x^2}{2!}+\cdots\right)+\left(\cdots +\frac{x^{-1/2}}{-1/2!}+\frac{x^{1/2}}{1/2!}+\frac{x^{3/2}}{3/2!}+\frac{x^{5/2}}{5/2!}+\cdots\right)$$
Therefore
$$D_x^{1/2}(e^x)=\cdots +\frac{x^{-5/2}}{-5/2!}+\frac{x^{-3/2}}{-3/2!}+\frac{x^{-1/2}}{-1/2!}+\frac{x^{1/2}}{1/2!}+\frac{x^{3/2}}{3/2!}+\frac{x^{5/2}}{5/2!}+\cdots$$
Unfortunately the half-order differentiation of $e^x$ is undefined by this series expansion.
AN OTHER PROOF
Let us assume that $D_x^{1/2}(e^{ax})=a^{1/2}e^{ax}$ that means:
$$D_x^{1/2}\left(\lim_{n \to \infty}(1+\frac1n)^{n(ax)}\right)=a^{1/2}\left(\lim_{n \to \infty}(1+\frac1n)^{n(ax)}\right)$$
And also by exponential property it can be written as:
$$D_x^{1/2}\left(\lim_{n \to \infty}(1+\frac anx)^{n}\right)=a^{1/2}\left(\lim_{n \to \infty}(1+\frac anx)^{n}\right)$$
Now the equation is under power role which seems to be ok for any integer-order differentioation.
Because $n$ is constant so it can be any positive real vlaue, and we expect the same result for any value of $n$.
Then for the first test $(n=1)$,
$$D_x^{1/2}\left((1+ ax)^{(1)}\right)=\frac{a^{1/2}}{\Gamma(3/2)}(1+ax)^{(\frac12)}$$
But if we solve it directly we get,
$$D_x^{1/2}\left(1+ ax\right)=\frac{x^{-1/2}}{\Gamma(1/2)}+a\frac{x^{1/2}}{\Gamma(3/2)}$$
And we can simply see that,
$$\frac{a^{1/2}}{\Gamma(3/2)}(1+ax)^{(\frac12)} \neq \frac{x^{-1/2}}{\Gamma(1/2)}+a\frac{x^{1/2}}{\Gamma(3/2)}$$
Hence the first test $"n=1"$ has failed.
FINALLY
Nevertheless there is a relation which says
$$D_x^{\alpha}(e^x)=e^x \cdot D_x^{\alpha}(e^x)|_{x=0}$$
Which I will prove it in one of the next posts (If God wills).
Tuesday, September 20, 2016
Refute the extension of "grünwald–letnikov derivative" to non-integers.
The claim that Grünwald–Letnikov derivative is valid for fractional calculus is disproved by this simple test:
Suppose that the first order differentiation is unknown or difficult to obtain as fractional calculus and also we can only calculate the differentiation at its even orders (the multiples of the second order differentiation)
The limit of the second order differentiation is:
$$\lim_{h \rightarrow 0}\frac {f(x+2h)-2f(x+h)+f(h)} {h^2}$$
By iterating this limit we can construct a formula looks like grünwald–letnikov derivative but it recognize the even order differentiation, so for example:
$$D^{2}e^{-x}=D^{4}e^{-x}=D^{6}e^{-x}=D^{8}e^{-x}=D^{10}e^{-x}=\cdots =D^{2n}e^{-x}=e^{-x}$$
This constructed formula will treat $e^{-x}$ as a neutral function for all its differentiation according to its mean value.
Then if we try to evaluate a non-even order differentiation of $e^{-x}$
We will get that $D^{1}e^{-x}=e^{-x}$ but this result is not true.
Hence the claim of extending grünwald–letnikov derivative to non-integer values is false.
Suppose that the first order differentiation is unknown or difficult to obtain as fractional calculus and also we can only calculate the differentiation at its even orders (the multiples of the second order differentiation)
The limit of the second order differentiation is:
$$\lim_{h \rightarrow 0}\frac {f(x+2h)-2f(x+h)+f(h)} {h^2}$$
By iterating this limit we can construct a formula looks like grünwald–letnikov derivative but it recognize the even order differentiation, so for example:
$$D^{2}e^{-x}=D^{4}e^{-x}=D^{6}e^{-x}=D^{8}e^{-x}=D^{10}e^{-x}=\cdots =D^{2n}e^{-x}=e^{-x}$$
This constructed formula will treat $e^{-x}$ as a neutral function for all its differentiation according to its mean value.
Then if we try to evaluate a non-even order differentiation of $e^{-x}$
We will get that $D^{1}e^{-x}=e^{-x}$ but this result is not true.
Hence the claim of extending grünwald–letnikov derivative to non-integer values is false.
Friday, September 16, 2016
Fractional Calculus of Zero
Zero in any differentiation or integration order can be expressed as (Zero summation formula).
$$D_{x}^{\alpha} (0)=\sum_{k=1}^{\infty}C_k\frac{x^{-(\alpha+k)}}{\Gamma(1-(\alpha+k))}$$
Where the summation terms are the values of Reciprocal gamma function at its roots for $\alpha = 0$ and $C_k$ is constant (See Reciprocal gamma function graph).
The zeros of Reciprocal gamma function are at $n$ where $-n \in \Bbb N$.
So for the first-order differentiation, it can be expressed as:
$$D_x^1f(x)=f'(x)+\sum_{k=1}^{\infty}C_k\frac{x^{-(1+k)}}{\Gamma(1-(1+k))}=f'(x)$$
This is the same first order differentiation and there is no need to set the constants to zero because this integer order of differentiation jumps from one zero of Reciprocal gamma function to another so all terms become zeros all time.
Now for the integration.
$$D_x^{-1}f(x)=g(x)+\sum_{k=1}^{\infty}C_k\frac{x^{-(-1+k)}}{\Gamma(1-(-1+k))}=g(x)+C_1 \frac{x^0}{\Gamma(1)}+\sum_{k=2}^{\infty}C_k\frac{x^{-(-1+k)}}{\Gamma(1-(-1+k))}$$
We can see a constant that need to be determined and that is the so-called integral constant which is usually set to zero as default.
So if we need to evaluate higher integration order, more constants comes out from zero summation formula need to be evaluated.
For example
$$D_x^{-3}f(x)=g(x)+\sum_{k=1}^{\infty}C_k\frac{x^{-(-3+k)}}{\Gamma(1-(-3+k))}=g(x)+C_1 \frac{x^2}{\Gamma(3)}+C_2 \frac{x}{\Gamma(2)}+C_3 \frac{x^0}{\Gamma(1)}+\sum_{k=4}^{\infty}C_k\frac{x^{-(-1+k)}}{\Gamma(1-(-1+k))}$$
And so on, the higher integration order the more constants and polynomial terms joining the integration result, but for a reason we set all these constants to zero.
Now let us see what happen if one wants to evaluate the half-order differentiation for a function.
$$D_x^{1/2}f(x)=g(x)+\sum_{k=1}^{\infty}C_k\frac{x^{-(\frac12+k)}}{\Gamma\left(1-(\frac12+k)\right)}$$
and if the function contains a constant
$$D_x^{1/2}\left(f(x)+C_0\right)=g(x)+C_0\frac{x^{-\frac12}}{\Gamma(\frac12)} +\sum_{k=1}^{\infty}C_k\frac{x^{-(\frac12+k)}}{\Gamma \left(1-(\frac12+k)\right)}$$
The zero summation formula is now a polynomial that diverges, making the half-order differentiation undefined at all, so for this reason and the same as integral constant reason we should set all these constants to zero.
Hence $$D_x^{1/2}(0)=0$$
$$D_{x}^{\alpha} (0)=\sum_{k=1}^{\infty}C_k\frac{x^{-(\alpha+k)}}{\Gamma(1-(\alpha+k))}$$
Where the summation terms are the values of Reciprocal gamma function at its roots for $\alpha = 0$ and $C_k$ is constant (See Reciprocal gamma function graph).
The zeros of Reciprocal gamma function are at $n$ where $-n \in \Bbb N$.
So for the first-order differentiation, it can be expressed as:
$$D_x^1f(x)=f'(x)+\sum_{k=1}^{\infty}C_k\frac{x^{-(1+k)}}{\Gamma(1-(1+k))}=f'(x)$$
This is the same first order differentiation and there is no need to set the constants to zero because this integer order of differentiation jumps from one zero of Reciprocal gamma function to another so all terms become zeros all time.
Now for the integration.
$$D_x^{-1}f(x)=g(x)+\sum_{k=1}^{\infty}C_k\frac{x^{-(-1+k)}}{\Gamma(1-(-1+k))}=g(x)+C_1 \frac{x^0}{\Gamma(1)}+\sum_{k=2}^{\infty}C_k\frac{x^{-(-1+k)}}{\Gamma(1-(-1+k))}$$
We can see a constant that need to be determined and that is the so-called integral constant which is usually set to zero as default.
So if we need to evaluate higher integration order, more constants comes out from zero summation formula need to be evaluated.
For example
$$D_x^{-3}f(x)=g(x)+\sum_{k=1}^{\infty}C_k\frac{x^{-(-3+k)}}{\Gamma(1-(-3+k))}=g(x)+C_1 \frac{x^2}{\Gamma(3)}+C_2 \frac{x}{\Gamma(2)}+C_3 \frac{x^0}{\Gamma(1)}+\sum_{k=4}^{\infty}C_k\frac{x^{-(-1+k)}}{\Gamma(1-(-1+k))}$$
And so on, the higher integration order the more constants and polynomial terms joining the integration result, but for a reason we set all these constants to zero.
Now let us see what happen if one wants to evaluate the half-order differentiation for a function.
$$D_x^{1/2}f(x)=g(x)+\sum_{k=1}^{\infty}C_k\frac{x^{-(\frac12+k)}}{\Gamma\left(1-(\frac12+k)\right)}$$
and if the function contains a constant
$$D_x^{1/2}\left(f(x)+C_0\right)=g(x)+C_0\frac{x^{-\frac12}}{\Gamma(\frac12)} +\sum_{k=1}^{\infty}C_k\frac{x^{-(\frac12+k)}}{\Gamma \left(1-(\frac12+k)\right)}$$
The zero summation formula is now a polynomial that diverges, making the half-order differentiation undefined at all, so for this reason and the same as integral constant reason we should set all these constants to zero.
Hence $$D_x^{1/2}(0)=0$$
Is the Power Tower has only one value?
Let $W=h(z)$
$h(z) = z\uparrow\uparrow n$ when n approaches to infinity.
its clear that:
$z^{h(z)} = h(z)$ then $z^w = w$
$w = \frac1 {(ssrt(1/z))}$ where $ssrt(x)$ is super square root of $x$.
$h(z) = \frac1 {(ssrt(1/z))}$
The super square root $ssrt(x)$ has one real value when $x > 1$, two real values for $e^{-\frac{1}{e}} < x < 1$ and imaginary values when $x < e^{-\frac{1}{e}}$.
Example:
$z=\sqrt{2}$
$h(\sqrt{2}) = \frac1 {ssrt\left(\frac1{\sqrt{2}}\right)}$
Note that $(\frac12)^{\frac12}=\frac1{\sqrt{2}}$ and also $(\frac14)^{\frac14}=\frac1{\sqrt{2}}$
Then $h(z)=h(\sqrt{2})=\frac1{\frac12}=2$
and also $h(z)=h(\sqrt{2})=\frac1{\frac14}=4$
$h(z) = z\uparrow\uparrow n$ when n approaches to infinity.
its clear that:
$z^{h(z)} = h(z)$ then $z^w = w$
$w = \frac1 {(ssrt(1/z))}$ where $ssrt(x)$ is super square root of $x$.
$h(z) = \frac1 {(ssrt(1/z))}$
The super square root $ssrt(x)$ has one real value when $x > 1$, two real values for $e^{-\frac{1}{e}} < x < 1$ and imaginary values when $x < e^{-\frac{1}{e}}$.
Example:
$z=\sqrt{2}$
$h(\sqrt{2}) = \frac1 {ssrt\left(\frac1{\sqrt{2}}\right)}$
Note that $(\frac12)^{\frac12}=\frac1{\sqrt{2}}$ and also $(\frac14)^{\frac14}=\frac1{\sqrt{2}}$
Then $h(z)=h(\sqrt{2})=\frac1{\frac12}=2$
and also $h(z)=h(\sqrt{2})=\frac1{\frac14}=4$
Tuesday, September 13, 2016
General formula for $(x+a)^{\frac 1x} =b$
Note that : this problem can be also solved by Lambert W-function, but I prefer this solution because it is similar to "Completing the square method" and the formula looks as if it was an elementary solution, also note that Lambert W-functions must have logarithm in its formula to solve this problem.
Solution:
This solution depends on the method that I call it "Completing the super square" because its steps looks like the known method of solving the quadratic equation.
By starting with.
$x + a = b^x$
Let $y = x + a$
Substitute $y$ in the equation
$y = b^{y-a} \Rightarrow y = \frac {b^y}{b^a} \Rightarrow b^a y = b^y \Rightarrow \frac {1}{b^a y} = b^{-y}$
Now powering both sides to $\frac {1}{b^a y}$ for eliminating $y$ in the right side and making same power same base for the left side.
$(\frac {1}{b^a y})^{\frac {1}{b^a y}} = (b^{-y} )^{\frac {1}{b^a y}}$
$(\frac {1}{b^a y})^{\frac {1}{b^a y}} = b^{-y*\frac {1}{b^a y}} = b^{\frac {-1}{b^a} }$
Getting the super square root of both sides
$\sqrt {(\frac {1}{b^a y})^{\frac {1}{b^a y}}}_{s} = {\sqrt {b^{\frac {-1}{b^a} }}}_{s}$
Where $\sqrt {(...)}_{s}$ is super square root, and because the base of the left side equal its power then it is easy to get super square root of it as below.
$\frac {1}{b^a y} = {\sqrt {b^{\frac {-1}{b^a} }}}_{s}$
$y=\frac {1}{b^a {\sqrt {b^{\frac {-1}{b^a} }}}_{s}}$
$x + a =\frac {1}{b^a {\sqrt {b^{\frac {-1}{b^a} }}}_{s}}$
Finally the general formula is
$$x = -a + \frac {1}{b^a {\sqrt {b^{(\frac {-1}{b^a}) }}}_{s}}$$
Example to test the formula:
$(x + 2)^{1/x} = 2$
Solution:
$x = -2 + \frac {1}{2^2 {\sqrt {2^{(\frac {-1}{2^2}) }}}_{s}} = -2 + \frac {1}{4 {\sqrt {2^{(\frac {-1}{4}) }}}_{s}} = -2 + \frac {1}{4 {\sqrt {\frac {1}{2^{(\frac {1}{4})}}}}_{s}}$
By calculating super square root values we obtain two real values.
${\sqrt {\frac {1}{2^{(\frac {1}{4})}}}}_{s} =\frac {1}{16} = 0.0625$ …… (because $0.0625^{0.0625}=0.8409=\frac {1}{2^{(\frac {1}{4})}}$ )
And
${\sqrt {\frac {1}{2^{(\frac {1}{4})}}}}_{s} = 0.8067$ …… (because $0.8067^{0.8067} = 0.8409 = \frac {1}{2^{(\frac {1}{4})}}$)
$x_{1}=-2 + \frac {1}{4*\frac {1}{16}} = -2 + 4 = 2$
$x_{2}=-2 + \frac {1}{4*0.8067}=-2 + 0.3099 = -1.6901$
Solution:
This solution depends on the method that I call it "Completing the super square" because its steps looks like the known method of solving the quadratic equation.
By starting with.
$x + a = b^x$
Let $y = x + a$
Substitute $y$ in the equation
$y = b^{y-a} \Rightarrow y = \frac {b^y}{b^a} \Rightarrow b^a y = b^y \Rightarrow \frac {1}{b^a y} = b^{-y}$
Now powering both sides to $\frac {1}{b^a y}$ for eliminating $y$ in the right side and making same power same base for the left side.
$(\frac {1}{b^a y})^{\frac {1}{b^a y}} = (b^{-y} )^{\frac {1}{b^a y}}$
$(\frac {1}{b^a y})^{\frac {1}{b^a y}} = b^{-y*\frac {1}{b^a y}} = b^{\frac {-1}{b^a} }$
Getting the super square root of both sides
$\sqrt {(\frac {1}{b^a y})^{\frac {1}{b^a y}}}_{s} = {\sqrt {b^{\frac {-1}{b^a} }}}_{s}$
Where $\sqrt {(...)}_{s}$ is super square root, and because the base of the left side equal its power then it is easy to get super square root of it as below.
$\frac {1}{b^a y} = {\sqrt {b^{\frac {-1}{b^a} }}}_{s}$
$y=\frac {1}{b^a {\sqrt {b^{\frac {-1}{b^a} }}}_{s}}$
$x + a =\frac {1}{b^a {\sqrt {b^{\frac {-1}{b^a} }}}_{s}}$
Finally the general formula is
$$x = -a + \frac {1}{b^a {\sqrt {b^{(\frac {-1}{b^a}) }}}_{s}}$$
Example to test the formula:
$(x + 2)^{1/x} = 2$
Solution:
$x = -2 + \frac {1}{2^2 {\sqrt {2^{(\frac {-1}{2^2}) }}}_{s}} = -2 + \frac {1}{4 {\sqrt {2^{(\frac {-1}{4}) }}}_{s}} = -2 + \frac {1}{4 {\sqrt {\frac {1}{2^{(\frac {1}{4})}}}}_{s}}$
By calculating super square root values we obtain two real values.
${\sqrt {\frac {1}{2^{(\frac {1}{4})}}}}_{s} =\frac {1}{16} = 0.0625$ …… (because $0.0625^{0.0625}=0.8409=\frac {1}{2^{(\frac {1}{4})}}$ )
And
${\sqrt {\frac {1}{2^{(\frac {1}{4})}}}}_{s} = 0.8067$ …… (because $0.8067^{0.8067} = 0.8409 = \frac {1}{2^{(\frac {1}{4})}}$)
$x_{1}=-2 + \frac {1}{4*\frac {1}{16}} = -2 + 4 = 2$
$x_{2}=-2 + \frac {1}{4*0.8067}=-2 + 0.3099 = -1.6901$
Numerical Grid for generating primes
This method is somehow an improvement of "Sieve of Eratosthenes" (Eratosthenes is ancient pentapolitan mathematician was born in Cyrene near my city.)
Here is a PDF file explains the method and the steps graphically.
Click here to download PDF file
Size (735.34 KB)
Click on the image to see an example of Filtering primes from 1 to 1000.

Here is a PDF file explains the method and the steps graphically.
Click here to download PDF file
Size (735.34 KB)
Click on the image to see an example of Filtering primes from 1 to 1000.
Monday, September 12, 2016
A New Method to Express Sums of Power of Integers as a Polynomial Equation
This is a new method to express The power sums of $(n^m)$ as a $(m+1)th-degree$ polynomial equation of n, there is some methods like "Faulhaber's formula" and others gives the solution of the power sums. nevertheless my method is doing the same but it does not depend on Bernoulli numbers or integrals as it is a simple algebraic way giving a polynomial equation and proved in a elementary algebraic logic.
And although I uploaded this paper in 2012 I found after that may be similar method on Wikipedia but this paper has interesting furmula and I hope you injoy reading its proof.
Click here to download the paper.
And although I uploaded this paper in 2012 I found after that may be similar method on Wikipedia but this paper has interesting furmula and I hope you injoy reading its proof.
Click here to download the paper.
The First Derivative Proof of tetration functions b^^x , x^^x and x^^f(x)
This paper is to find by proof the first derive of known tetration functions, fixed base iterated functions $b\uparrow \uparrow x$ , general case for $b\uparrow \uparrow f(x)$ and variable base with variable height iterated function $x\uparrow \uparrow x$. although the case of $b\uparrow \uparrow x$ is already known by using the base change method but its derive function $f(x)$ is still depend on the derive of $f(x-1)$ which gives a shortcoming derivation. However, in the coming proofs, the resulted derivative functions are proved by applying differentiation elementary concepts step by step up to the final first derive ,but an unknown limit and a non-elementary product part of the resulted derivative function still needs study, Although I included approximation method for numerical solutions.
Click here to download the paper
Click here to download the paper
Saturday, September 10, 2016
Does ssrt(x) = x^^(1/2)
Notations:
$ssrt(x) = \sqrt {x}_s$ (Super Square Root).
x^^(1/2) $= ^{\frac 12}x$ (half fractional tetrations).
Does $ \sqrt {x}_s = ^{\frac 12}x$?
Actually no.
because that means
If $a = ^{b}n$ then $n = ^{\frac 1b}a$
Let us assume that is true.
if $ ^{n}x = z$ , n aproaches to infinity.
Then $x = ^{\frac 1n}z= ^{0}z$
As a fact, we already know that
$ ^{0}z$ is always equal to $1$.
but $x = z^{\frac 1z}$.
Hence the result is $^{0}z = ^{\frac 1z}z$ and that is not true.
Therefore the assumption has failed.
$ssrt(x) = \sqrt {x}_s$ (Super Square Root).
x^^(1/2) $= ^{\frac 12}x$ (half fractional tetrations).
Does $ \sqrt {x}_s = ^{\frac 12}x$?
Actually no.
because that means
If $a = ^{b}n$ then $n = ^{\frac 1b}a$
Let us assume that is true.
if $ ^{n}x = z$ , n aproaches to infinity.
Then $x = ^{\frac 1n}z= ^{0}z$
As a fact, we already know that
$ ^{0}z$ is always equal to $1$.
but $x = z^{\frac 1z}$.
Hence the result is $^{0}z = ^{\frac 1z}z$ and that is not true.
Therefore the assumption has failed.
Divisors of integers new function
Assume that
$$a*b = n , n \in \Bbb N \tag 1$$
There is unlimited solutions for this equation, because no restrictions for this equation to consider $a$ & $b$ as integers.
So how can we make it forcing $a$ & $b$ always as integers?
Here is the method:
As we know that $sin(\pi \cdot a) = 0$ only when $a$ is integer.
and we also know that $x^2 +y^2=0$ only when $x=0$ & $y=0$ provided that $x$ and $y$ are always real.
So we can say:
$sin(\pi \cdot a) = 0$
$sin(\pi \cdot b) = 0$
Let $x=sin(\pi \cdot a)$ and $y=sin(\pi \cdot b)$.
then $sin^2(\pi \cdot a) +sin^2(\pi \cdot b) = 0 \tag 2$
from equation $(1)$ we get
$b = \frac na$
substitute it in equation $(2)$
$sin^2(\pi \cdot a) +sin^2(\pi \cdot \frac na) = 0 \tag 3$
Now we have a equation that $a$ must be a devisor of $n$.
Here is the final formula
$$f(n,a)=sin^2(\pi \cdot a) +sin^2(\pi \cdot \frac na)$$
we can also substitute $sin(\pi \cdot a)$ by Euler reflection formula
$$\Gamma(a) \Gamma(1-a)=\frac {\pi}{sin(\pi \cdot a)}$$
Try to give integer values for $n$ and draw the function, you will see that the roots of this function are the divisors of $n$ that when $f(n,a) = 0$.
$$a*b = n , n \in \Bbb N \tag 1$$
There is unlimited solutions for this equation, because no restrictions for this equation to consider $a$ & $b$ as integers.
So how can we make it forcing $a$ & $b$ always as integers?
Here is the method:
As we know that $sin(\pi \cdot a) = 0$ only when $a$ is integer.
and we also know that $x^2 +y^2=0$ only when $x=0$ & $y=0$ provided that $x$ and $y$ are always real.
So we can say:
$sin(\pi \cdot a) = 0$
$sin(\pi \cdot b) = 0$
Let $x=sin(\pi \cdot a)$ and $y=sin(\pi \cdot b)$.
then $sin^2(\pi \cdot a) +sin^2(\pi \cdot b) = 0 \tag 2$
from equation $(1)$ we get
$b = \frac na$
substitute it in equation $(2)$
$sin^2(\pi \cdot a) +sin^2(\pi \cdot \frac na) = 0 \tag 3$
Now we have a equation that $a$ must be a devisor of $n$.
Here is the final formula
$$f(n,a)=sin^2(\pi \cdot a) +sin^2(\pi \cdot \frac na)$$
we can also substitute $sin(\pi \cdot a)$ by Euler reflection formula
$$\Gamma(a) \Gamma(1-a)=\frac {\pi}{sin(\pi \cdot a)}$$
Try to give integer values for $n$ and draw the function, you will see that the roots of this function are the divisors of $n$ that when $f(n,a) = 0$.
Friday, September 9, 2016
Symmetry method to find Primes.
By observation I found this method to find primes which can be proofed easily.
For every $p_n$ & $a$ that satisfy $p_n < p_n\#-a < p_{n+1}^2$ where $(a > p_n)$
If $(a)$ is a prime then $(p_n\#-a)$ is also a prime
and if $(p_n\#-a)$ is a prime then $(a)$ is possible a prime
Example:
$a=2213$ (prime number)
let $p_n$ any prime satisfy the above
for instance $p_5=11$ then $p_5\#=2310$
$11<2310-2213<13*13$
$11<97<169$ it's OK
Then 97 must be a prime.
$(a)$ and $(p_n\#-a)$ are symmetrical around $\frac {p_n\#}{2}$
Let $a=\frac {p_n\#}{2}+b$ then $(p_n\#-a)=\frac {p_n\#}{2}-b$
$p_n\#=(\frac {p_n\#}{2}+b)+(\frac {p_n\#}{2}-b)$
assume that $(\frac {p_n\#}{2}+b)$ is divisible by $\{p_k : p_k \le p_n\}$
then $(\frac {p_n\#}{2}-b)$ must be divisible by $p_k$ too
because $\frac {p_n\#}{2}$ is always divisible by any prime $2 < p_k \le p_n$ so if $(+b)$ is divisible by $p_k$ then $(-b)$ is divisible as well. and if $(\frac {p_n\#}{2}+b)$ is not divisible by any prime of $\{p_k : p_k \le p_n\}$ then $(\frac {p_n\#}{2}-b)$ should be also not divisible by the same prime. So we have this range which we can define the symmetry of the numbers that are not divisible by $\{p_k : p_k \le p_n\}$. that range is from $(p_n+1)$ to $(p_n\#-(p_n+1))$ then $a$ should always greater than $p_n$ $(a > p_n)$
but unfortunately this range of symmetry is broken by the primes greater than $p_n$ because $p_n\#$ is not divisible by $p_{n+1}$ and greater.
So the limits of symmetry ,which can not be affected by the primes greater than $p_n$ , can be defined between $p_n$ and $p_{n+1}^2$
So if $(p_n\#-a)$ satisfy $p_n \lt p_n\#-a \lt p_{n+1}^2$ then it is in the range of symmetry and if $(a)$ is prime then $(p_n\#-a)$ is also prime
but if $(p_n\#-a)$ is prime then $(a)$ could be prime because it will not be divisible by $\{ p_k : p_k \le p_n\}$ but on the other hand it could be divisible by the primes greater than $p_n$ because it is may located out of the range where the symmetry is broken.
We can notice the symmetry in these extra examples
1) For $p_3\#=2*3*5=30$
$p_{n+1}^2=7∗7=49$
so all the primes $5 < p < 30$ are symmetrical around 15 $\frac {p_n\#}{2}=15$ note that $15±2 , 15±4 , 15±8$ are all primes.
2) For $p_4=210$ $p_{n+1}^2=11∗11=121$, number $121$ is less than $210$ which will break the symmetry starting from $121$ so the range that will maintain the symmetry is $(7 < 210-a < 121)$ , $a > 7$
$\frac {p_n\#}{2}=105$ note that $105±2 , 105±4 , 105±8$ are primes etc...
Let $a=151$ (prime number) then $210-151=59$
$7 < 59 < 121$ then $59$ is a prime.
THEOREM
For every $p_n$ & $a$ that satisfy $p_n < p_n\#-a < p_{n+1}^2$ where $(a > p_n)$
If $(a)$ is a prime then $(p_n\#-a)$ is also a prime
and if $(p_n\#-a)$ is a prime then $(a)$ is possible a prime
Example:
$a=2213$ (prime number)
let $p_n$ any prime satisfy the above
for instance $p_5=11$ then $p_5\#=2310$
$11<2310-2213<13*13$
$11<97<169$ it's OK
Then 97 must be a prime.
THE PROOF
$(a)$ and $(p_n\#-a)$ are symmetrical around $\frac {p_n\#}{2}$
Let $a=\frac {p_n\#}{2}+b$ then $(p_n\#-a)=\frac {p_n\#}{2}-b$
$p_n\#=(\frac {p_n\#}{2}+b)+(\frac {p_n\#}{2}-b)$
assume that $(\frac {p_n\#}{2}+b)$ is divisible by $\{p_k : p_k \le p_n\}$
then $(\frac {p_n\#}{2}-b)$ must be divisible by $p_k$ too
because $\frac {p_n\#}{2}$ is always divisible by any prime $2 < p_k \le p_n$ so if $(+b)$ is divisible by $p_k$ then $(-b)$ is divisible as well. and if $(\frac {p_n\#}{2}+b)$ is not divisible by any prime of $\{p_k : p_k \le p_n\}$ then $(\frac {p_n\#}{2}-b)$ should be also not divisible by the same prime. So we have this range which we can define the symmetry of the numbers that are not divisible by $\{p_k : p_k \le p_n\}$. that range is from $(p_n+1)$ to $(p_n\#-(p_n+1))$ then $a$ should always greater than $p_n$ $(a > p_n)$
but unfortunately this range of symmetry is broken by the primes greater than $p_n$ because $p_n\#$ is not divisible by $p_{n+1}$ and greater.
So the limits of symmetry ,which can not be affected by the primes greater than $p_n$ , can be defined between $p_n$ and $p_{n+1}^2$
So if $(p_n\#-a)$ satisfy $p_n \lt p_n\#-a \lt p_{n+1}^2$ then it is in the range of symmetry and if $(a)$ is prime then $(p_n\#-a)$ is also prime
but if $(p_n\#-a)$ is prime then $(a)$ could be prime because it will not be divisible by $\{ p_k : p_k \le p_n\}$ but on the other hand it could be divisible by the primes greater than $p_n$ because it is may located out of the range where the symmetry is broken.
We can notice the symmetry in these extra examples
1) For $p_3\#=2*3*5=30$
$p_{n+1}^2=7∗7=49$
so all the primes $5 < p < 30$ are symmetrical around 15 $\frac {p_n\#}{2}=15$ note that $15±2 , 15±4 , 15±8$ are all primes.
2) For $p_4=210$ $p_{n+1}^2=11∗11=121$, number $121$ is less than $210$ which will break the symmetry starting from $121$ so the range that will maintain the symmetry is $(7 < 210-a < 121)$ , $a > 7$
$\frac {p_n\#}{2}=105$ note that $105±2 , 105±4 , 105±8$ are primes etc...
Let $a=151$ (prime number) then $210-151=59$
$7 < 59 < 121$ then $59$ is a prime.
Subscribe to:
Comments (Atom)