The Binomial Theorem proof by exponentials.

The famous furmula for the binomial is
$$(a+b)^n=\sum_{k=0}^{\infty} \binom nk a^k b^{n-k}$$
But we can also express the formula like this
$${(a+b)^n \over n!}=\sum_{k \in \Bbb Z} \frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!}$$
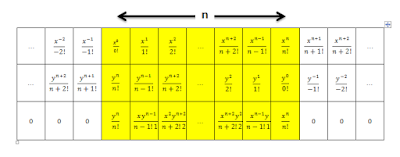
Actually the binomial structure is coming from the $nth$ term when multiplying two exponentials together , see the following picture.

Click on the image to enlarge it

The first row of the table is $e^x$ terms, the second row is $e^y$ terms arranged backwards and the last row is the result of multiplying every term from the first row by the opposite term in the second row.

The distance $n$ is from the zero term of the first row $e^x$ to the zero term of the second row $e^y$

So we can prove the binomial theorem by the following steps:
$$e^{a+b}=e^a e^b \tag1$$
$$\sum_{n \in \Bbb Z} \frac {(a+b)^n}{n!}=\left(\sum_{n \in \Bbb Z} \frac {a^n}{n!} \right) \left( \sum_{n \in \Bbb Z} \frac {b^n}{n!}\right) \tag2$$
We can use "Cauchy product of two infinite series" to multiply the two series in RHS in $eq(2)$.
$$\left(\sum_{n \in \Bbb Z} \frac {a^n}{n!} \right) \left( \sum_{n \in \Bbb Z} \frac {b^n}{n!}\right)=\sum_{n \in \Bbb Z}\left( \sum_{k \in \Bbb Z}\frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!} \right) \tag3$$
From $eq(2)$ & $eq(3)$ we get:
$$\sum_{n \in \Bbb Z} \frac {(a+b)^n}{n!}=\sum_{n \in \Bbb Z}\left( \sum_{k \in \Bbb Z}\frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!} \right) \tag4$$
Now it is clearly that every term of the series in the LHS is equal to the same $nth$ term in the RHS.

So we finally have
$${(a+b)^n \over n!}=\sum_{k \in \Bbb Z} \frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!} \tag5$$
Which indeed the same known binomial formula:
$$(a+b)^n=\sum_{k=0}^{\infty} \binom nk a^k b^{n-k}$$