The Binomial Theorem proof by exponentials.

The famous furmula for the binomial is
$$(a+b)^n=\sum_{k=0}^{\infty} \binom nk a^k b^{n-k}$$
But we can also express the formula like this
$${(a+b)^n \over n!}=\sum_{k \in \Bbb Z} \frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!}$$
Actually the binomial structure is coming from the $nth$ term when multiplying two exponentials together , see the following picture.

Click on the image to enlarge it

The first row of the table is $e^x$ terms, the second row is $e^y$ terms arranged backwards and the last row is the result of multiplying every term from the first row by the opposite term in the second row.

The distance $n$ is from the zero term of the first row $e^x$ to the zero term of the second row $e^y$

So we can prove the binomial theorem by the following steps:
$$e^{a+b}=e^a e^b \tag1$$
$$\sum_{n \in \Bbb Z} \frac {(a+b)^n}{n!}=\left(\sum_{n \in \Bbb Z} \frac {a^n}{n!} \right) \left( \sum_{n \in \Bbb Z} \frac {b^n}{n!}\right) \tag2$$
We can use "Cauchy product of two infinite series" to multiply the two series in RHS in $eq(2)$.
$$\left(\sum_{n \in \Bbb Z} \frac {a^n}{n!} \right) \left( \sum_{n \in \Bbb Z} \frac {b^n}{n!}\right)=\sum_{n \in \Bbb Z}\left( \sum_{k \in \Bbb Z}\frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!} \right) \tag3$$
From $eq(2)$ & $eq(3)$ we get:
$$\sum_{n \in \Bbb Z} \frac {(a+b)^n}{n!}=\sum_{n \in \Bbb Z}\left( \sum_{k \in \Bbb Z}\frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!} \right) \tag4$$
Now it is clearly that every term of the series in the LHS is equal to the same $nth$ term in the RHS.

So we finally have
$${(a+b)^n \over n!}=\sum_{k \in \Bbb Z} \frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!} \tag5$$
Which indeed the same known binomial formula:
$$(a+b)^n=\sum_{k=0}^{\infty} \binom nk a^k b^{n-k}$$

Disproving of $\frac{d^{1/2}}{dx^{1/2}}e^x = e^x$ with explanation.

Its clear that the devirative of $e^x$ equal itself for the integer order differentiation.
So does it means that it is allowed to equal itself for the half order as well?
Have you asked yourself if there is a function equal itself only every $even$ order or every $nth$ order throughout its multiples?

See the behavior of the following functions where $n \in \Bbb Z$
1) $D^{n}_x( e^x)=e^x $ (neutral function of integer-order Diffrentiation)
2) $D^{2n}_x\left(\frac{e^x+e^{-x}}{2}\right )=\frac{e^x+e^{-x}}{2}$ (neutral function of only even-order Diffrentiation)
3) $D^{3n}_x\left(\frac {e^x+e^{\omega x}+e^{\omega^2 x}}{3}\right)=\frac {e^x+e^{\omega x}+e^{\omega^2 x}}{3}$ where $\omega=e^{\frac{\pi i}{3}}$ (neutral function of only multiples-of-3-order Diffrentiation)
4) $D^{4n}_x\left(\frac {e^x+e^{-x}+e^{ix}+e^{-ix}}{4}\right)=\frac {e^x+e^{-x}+e^{ix}+e^{-ix}}{4}$ (neutral function of only multiples-of-4-order Diffrentiation)
and so on...

These belong to exponential k step $\sum_{k \in \Bbb Z}\frac{x^{nk}}{(nk)!}$ any every function of them can not equal itself with an order out of its $nth$ order and its multiples.
(Exponential k step has a formula for generating any k step  , $\sum_{k \in \Bbb Z}\frac{x^{nk}}{(nk)!}=\frac1k\sum_{j=1}^{k}e^{r^j_k x}$ where $r_k=e^{\frac{2\pi i}{k}}$)

Now let us rearrange the functions in other patern.
In the following steps I will use Mittag-Leffler function instead of k step sum but with little change as:
$$E_{\alpha}(x^{\alpha})=\sum_{k \in \Bbb Z}\frac{x^{\alpha k}}{(\alpha k)!} , \alpha >0 \tag 1$$
1) For $\alpha=1$ , $E_{1}(x)=e^x$
2) For $\alpha =2$ , $E_{2}(x^2)=\frac12(e^x+e^{-x})$
3) For $\alpha =4$ , $E_{4}(x^4)=\frac14(e^x+e^{-x}+e^{ix}+e^{-ix})$
4) For $\alpha =8$ , $E_{8}(x^8)=\frac18(e^x+e^{-x}+e^{ix}+e^{-ix}+e^{(i+1)x}+e^{(i-1)x}+e^{(-i+1)x}+e^{(-i-1)x})$

and so on every $2^n$ itration

We can obseve two relations
$$E_{2\alpha}(x^{2\alpha})=\frac12\left(E_{\alpha}(x^{\alpha})+E_{\alpha}\left((-1)^{\frac1{\alpha}}x^{\alpha}\right)\right) \tag 2$$
and
$$E_{\alpha}(x^{\alpha})=E_{2\alpha}(x^{2\alpha})+D_x^{\alpha}\left(E_{2\alpha}(x^{2\alpha})\right) \tag 3$$
For example:
$E_1(x)=E_2(x^2)+D^1_x(E_2(x^2))$
$=\frac12(e^x+e^{-x})+D^1_x\left(\frac12(e^x+e^{-x})\right)$
$=\frac12(e^x+e^{-x})+\frac12(e^x-e^{-x})=e^x$
Now if we let $\alpha = \frac12$ then
$E_{1/2}(x^{1/2})=E_1(x)+D_x^{1/2}(E_1(x))$
$=e^x+D_x^{1/2}(e^x)$

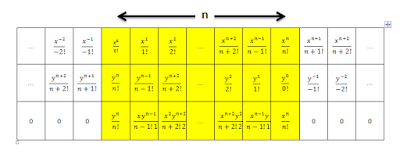
From eq(1) we have $$E_{1/2}(x^{1/2})=\sum_{k \in \Bbb Z}\frac{x^{\frac12 k}}{(\frac12 k)!}=\cdots +\frac{x^{-1}}{-1!}+\frac{x^{-1/2}}{-1/2!}+\frac{x^0}{0!}+\frac{x^{1/2}}{1/2!}+\frac{x^1}{1!}+\frac{x^{3/2}}{3/2!}+\frac{x^2}{2!}+\frac{x^{5/2}}{5/2!}+\cdots$$
Then
$$e^x+D_x^{1/2}(e^x)=\left(\cdots +\frac{x^{-1}}{-1!}+\frac{x^0}{0!}+\frac{x}{1!}+\frac{x^2}{2!}+\cdots\right)+\left(\cdots +\frac{x^{-1/2}}{-1/2!}+\frac{x^{1/2}}{1/2!}+\frac{x^{3/2}}{3/2!}+\frac{x^{5/2}}{5/2!}+\cdots\right)$$
Therefore
$$D_x^{1/2}(e^x)=\cdots +\frac{x^{-5/2}}{-5/2!}+\frac{x^{-3/2}}{-3/2!}+\frac{x^{-1/2}}{-1/2!}+\frac{x^{1/2}}{1/2!}+\frac{x^{3/2}}{3/2!}+\frac{x^{5/2}}{5/2!}+\cdots$$
Unfortunately the half-order differentiation of $e^x$ is undefined by this series expansion.

AN OTHER PROOF

Let us assume that $D_x^{1/2}(e^{ax})=a^{1/2}e^{ax}$ that means:
$$D_x^{1/2}\left(\lim_{n \to \infty}(1+\frac1n)^{n(ax)}\right)=a^{1/2}\left(\lim_{n \to \infty}(1+\frac1n)^{n(ax)}\right)$$
And also by exponential property it can be written as:
$$D_x^{1/2}\left(\lim_{n \to \infty}(1+\frac anx)^{n}\right)=a^{1/2}\left(\lim_{n \to \infty}(1+\frac anx)^{n}\right)$$
Now the equation is under power role which seems to be ok for any integer-order differentioation.
Because $n$ is constant so it can be any positive real vlaue, and we expect the same result for any value of $n$.
Then for the first test $(n=1)$,
$$D_x^{1/2}\left((1+ ax)^{(1)}\right)=\frac{a^{1/2}}{\Gamma(3/2)}(1+ax)^{(\frac12)}$$
But if we solve it directly we get,
 $$D_x^{1/2}\left(1+ ax\right)=\frac{x^{-1/2}}{\Gamma(1/2)}+a\frac{x^{1/2}}{\Gamma(3/2)}$$
And we can simply see that,
$$\frac{a^{1/2}}{\Gamma(3/2)}(1+ax)^{(\frac12)} \neq \frac{x^{-1/2}}{\Gamma(1/2)}+a\frac{x^{1/2}}{\Gamma(3/2)}$$
Hence the first test $"n=1"$ has failed.

FINALLY

Nevertheless there is a relation which says
$$D_x^{\alpha}(e^x)=e^x \cdot D_x^{\alpha}(e^x)|_{x=0}$$
Which I will prove it in one of the next posts (If God wills).

Refute the extension of "grünwald–letnikov derivative" to non-integers.

The claim that Grünwald–Letnikov derivative is valid for fractional calculus is disproved by this simple test:

Suppose that the first order differentiation is unknown or difficult to obtain as fractional calculus and also we can only calculate the differentiation at its even orders (the multiples of the second order differentiation)
The limit of the second order differentiation is:
$$\lim_{h \rightarrow 0}\frac {f(x+2h)-2f(x+h)+f(h)} {h^2}$$
By iterating this limit we can construct a formula looks like grünwald–letnikov derivative but it recognize the even order differentiation, so for example:
$$D^{2}e^{-x}=D^{4}e^{-x}=D^{6}e^{-x}=D^{8}e^{-x}=D^{10}e^{-x}=\cdots =D^{2n}e^{-x}=e^{-x}$$
This constructed formula will treat $e^{-x}$ as a neutral function for all its differentiation according to its mean value.
Then if we try to evaluate a non-even order differentiation of $e^{-x}$
We will get that $D^{1}e^{-x}=e^{-x}$ but this result is not true.

Hence the claim of extending grünwald–letnikov derivative to non-integer values is false.

Fractional Calculus of Zero

Zero in any differentiation or integration order can be expressed as (Zero summation formula).
$$D_{x}^{\alpha} (0)=\sum_{k=1}^{\infty}C_k\frac{x^{-(\alpha+k)}}{\Gamma(1-(\alpha+k))}$$
Where the summation terms are the values of Reciprocal gamma function at its roots for $\alpha = 0$ and $C_k$ is constant (See Reciprocal gamma function graph).
The zeros of Reciprocal gamma function are at $n$ where $-n \in \Bbb N$.
So for the first-order differentiation, it can be expressed as:
$$D_x^1f(x)=f'(x)+\sum_{k=1}^{\infty}C_k\frac{x^{-(1+k)}}{\Gamma(1-(1+k))}=f'(x)$$
This is the same first order differentiation and there is no need to set the constants to zero because this integer order of differentiation jumps from one zero of Reciprocal gamma function to another so all terms become zeros all time.
Now for the integration.
$$D_x^{-1}f(x)=g(x)+\sum_{k=1}^{\infty}C_k\frac{x^{-(-1+k)}}{\Gamma(1-(-1+k))}=g(x)+C_1 \frac{x^0}{\Gamma(1)}+\sum_{k=2}^{\infty}C_k\frac{x^{-(-1+k)}}{\Gamma(1-(-1+k))}$$
We can see a constant that need to be determined and that is the so-called integral constant which is usually set to zero as default.
So if we need to evaluate higher integration order, more constants comes out from zero summation formula need to be evaluated.
For example
$$D_x^{-3}f(x)=g(x)+\sum_{k=1}^{\infty}C_k\frac{x^{-(-3+k)}}{\Gamma(1-(-3+k))}=g(x)+C_1 \frac{x^2}{\Gamma(3)}+C_2 \frac{x}{\Gamma(2)}+C_3 \frac{x^0}{\Gamma(1)}+\sum_{k=4}^{\infty}C_k\frac{x^{-(-1+k)}}{\Gamma(1-(-1+k))}$$
And so on, the higher integration order the more constants and polynomial terms joining the integration result, but for a reason we set all these constants to zero.
Now let us see what happen if one wants to evaluate the half-order differentiation for a function.
$$D_x^{1/2}f(x)=g(x)+\sum_{k=1}^{\infty}C_k\frac{x^{-(\frac12+k)}}{\Gamma\left(1-(\frac12+k)\right)}$$
and if the function contains a constant
$$D_x^{1/2}\left(f(x)+C_0\right)=g(x)+C_0\frac{x^{-\frac12}}{\Gamma(\frac12)} +\sum_{k=1}^{\infty}C_k\frac{x^{-(\frac12+k)}}{\Gamma \left(1-(\frac12+k)\right)}$$
The zero summation formula is now a polynomial that diverges, making the half-order differentiation undefined at all, so for this reason and the same as integral constant reason we should set all these constants to zero.
Hence $$D_x^{1/2}(0)=0$$

Is the Power Tower has only one value?

Let $W=h(z)$
$h(z) = z\uparrow\uparrow n$ when n approaches to infinity.
its clear that:
$z^{h(z)} = h(z)$ then $z^w = w$
$w = \frac1 {(ssrt(1/z))}$ where $ssrt(x)$ is super square root of $x$.
$h(z) = \frac1 {(ssrt(1/z))}$

The super square root $ssrt(x)$ has one real value when $x > 1$, two real values for $e^{-\frac{1}{e}} < x < 1$ and imaginary values when $x < e^{-\frac{1}{e}}$.

Example:

$z=\sqrt{2}$
$h(\sqrt{2}) = \frac1 {ssrt\left(\frac1{\sqrt{2}}\right)}$
Note that $(\frac12)^{\frac12}=\frac1{\sqrt{2}}$ and also $(\frac14)^{\frac14}=\frac1{\sqrt{2}}$

Then $h(z)=h(\sqrt{2})=\frac1{\frac12}=2$
and also $h(z)=h(\sqrt{2})=\frac1{\frac14}=4$

General formula for $(x+a)^{\frac 1x} =b$

Note that : this problem can be also solved by Lambert W-function, but I prefer this solution because it is similar to "Completing the square method" and the formula looks as if it was an elementary solution, also note that Lambert W-functions must have logarithm in its formula to solve this problem.

Solution:
This solution depends on the method that I call it "Completing the super square" because its steps looks like the known method of solving the quadratic equation.

By starting with.
$x + a = b^x$
Let  $y = x + a$
Substitute $y$ in the equation
$y = b^{y-a} \Rightarrow y = \frac {b^y}{b^a}  \Rightarrow b^a y = b^y \Rightarrow \frac {1}{b^a y} = b^{-y}$
Now powering both sides to $\frac {1}{b^a y}$ for eliminating $y$ in the right side and making same power same base for the left side.
$(\frac {1}{b^a y})^{\frac {1}{b^a y}} = (b^{-y} )^{\frac {1}{b^a y}}$

$(\frac {1}{b^a y})^{\frac {1}{b^a y}} = b^{-y*\frac {1}{b^a y}} = b^{\frac {-1}{b^a} }$
Getting the super square root of both sides
$\sqrt {(\frac {1}{b^a y})^{\frac {1}{b^a y}}}_{s} = {\sqrt {b^{\frac {-1}{b^a} }}}_{s}$
Where $\sqrt {(...)}_{s}$  is super square root, and because the base of the left side equal its power then it is easy to get super square root of it as below.
$\frac {1}{b^a y} = {\sqrt {b^{\frac {-1}{b^a} }}}_{s}$
$y=\frac {1}{b^a {\sqrt {b^{\frac {-1}{b^a} }}}_{s}}$
$x + a =\frac {1}{b^a {\sqrt {b^{\frac {-1}{b^a} }}}_{s}}$

Finally the general formula is
$$x = -a + \frac {1}{b^a {\sqrt {b^{(\frac {-1}{b^a}) }}}_{s}}$$
Example to test the formula:
$(x + 2)^{1/x} = 2$

Solution:
$x = -2 + \frac {1}{2^2 {\sqrt {2^{(\frac {-1}{2^2}) }}}_{s}} = -2 + \frac {1}{4 {\sqrt {2^{(\frac {-1}{4}) }}}_{s}} = -2 + \frac {1}{4 {\sqrt {\frac {1}{2^{(\frac {1}{4})}}}}_{s}}$
By calculating super square root values we obtain two real values.
${\sqrt {\frac {1}{2^{(\frac {1}{4})}}}}_{s} =\frac {1}{16} = 0.0625$ …… (because $0.0625^{0.0625}=0.8409=\frac {1}{2^{(\frac {1}{4})}}$ )
And
${\sqrt {\frac {1}{2^{(\frac {1}{4})}}}}_{s} = 0.8067$  …… (because $0.8067^{0.8067} = 0.8409 = \frac {1}{2^{(\frac {1}{4})}}$) 
$x_{1}=-2 + \frac {1}{4*\frac {1}{16}} = -2 + 4 = 2$

$x_{2}=-2 + \frac {1}{4*0.8067}=-2 + 0.3099 = -1.6901$

Numerical Grid for generating primes

This method is somehow an improvement of "Sieve of Eratosthenes" (Eratosthenes is ancient pentapolitan mathematician was born in Cyrene near my city.)
Here is a PDF file explains the method and the steps graphically.

Click here to download PDF file

Size (735.34 KB)

Click on the image to see an example of Filtering primes from 1 to 1000.

A New Method to Express Sums of Power of Integers as a Polynomial Equation

This is a new method to express The power sums of $(n^m)$ as a $(m+1)th-degree$ polynomial equation of n, there is some methods like "Faulhaber's formula" and others gives the solution of the power sums. nevertheless my method is doing the same but it does not depend on Bernoulli numbers or integrals as it is a simple algebraic way giving a polynomial equation and proved in a elementary algebraic logic.
And although I uploaded this paper in 2012 I found after that may be similar method on Wikipedia but this paper has interesting furmula and I hope you injoy reading its proof.

Click here to download the paper.

The First Derivative Proof of tetration functions b^^x , x^^x and x^^f(x)

This paper is to find by proof the first derive of known tetration functions, fixed base iterated functions $b\uparrow \uparrow x$ , general case for $b\uparrow \uparrow f(x)$ and variable base with variable height iterated function $x\uparrow \uparrow x$. although the case of $b\uparrow \uparrow x$ is already known by using the base change method but its derive function $f(x)$ is still depend on the derive of $f(x-1)$ which gives a shortcoming derivation. However, in the coming proofs, the resulted derivative functions are proved by applying differentiation elementary concepts step by step up to the final first derive ,but an unknown limit and a non-elementary product part of the resulted derivative function still needs study, Although I included approximation method for numerical solutions.

Click here to download the paper

Does ssrt(x) = x^^(1/2)

Notations:
$ssrt(x) = \sqrt {x}_s$  (Super Square Root).
x^^(1/2) $= ^{\frac 12}x$  (half fractional tetrations).

Does $ \sqrt {x}_s =  ^{\frac 12}x$?
Actually no.
because that means
If $a =  ^{b}n$  then $n =  ^{\frac 1b}a$

Let us assume that is true.
if $ ^{n}x = z$ , n aproaches to infinity.
Then $x =  ^{\frac 1n}z=  ^{0}z$
As a fact, we already know that
$ ^{0}z$ is always equal to $1$.
but $x = z^{\frac 1z}$.
Hence the result is $^{0}z = ^{\frac 1z}z$ and that is not true.
Therefore the assumption has failed.

Divisors of integers new function

Assume that
$$a*b = n , n \in \Bbb N \tag 1$$

There is unlimited solutions for this equation, because no restrictions for this equation to consider $a$ & $b$ as integers.

So how can we make it forcing $a$ & $b$ always as integers?

Here is the method:

As we know that $sin(\pi \cdot a) = 0$ only when $a$ is integer.
and we also know that $x^2 +y^2=0$ only when $x=0$ & $y=0$ provided that $x$ and $y$ are always real.
So we can say:
$sin(\pi \cdot a) = 0$
$sin(\pi \cdot b) = 0$

Let $x=sin(\pi \cdot a)$ and $y=sin(\pi \cdot b)$.

then $sin^2(\pi \cdot a) +sin^2(\pi \cdot b) = 0 \tag 2$

from equation $(1)$ we get
 $b = \frac na$
substitute it in equation $(2)$

 $sin^2(\pi \cdot a) +sin^2(\pi \cdot \frac na) = 0 \tag 3$

Now we have a equation that $a$ must be a devisor of $n$.

Here is the final formula
$$f(n,a)=sin^2(\pi \cdot a) +sin^2(\pi \cdot \frac na)$$

we can also substitute $sin(\pi \cdot a)$ by Euler reflection formula
$$\Gamma(a) \Gamma(1-a)=\frac {\pi}{sin(\pi \cdot a)}$$
Try to give integer values for $n$ and draw the function, you will see that the roots of this function are the divisors of $n$ that when $f(n,a) = 0$.

Symmetry method to find Primes.

By observation I found this method to find primes which can be proofed easily.

THEOREM

For every $p_n$ & $a$ that satisfy $p_n < p_n\#-a < p_{n+1}^2$ where $(a > p_n)$

If $(a)$ is a prime then $(p_n\#-a)$ is also a prime

and if $(p_n\#-a)$ is a prime then $(a)$ is possible a prime

Example:
$a=2213$ (prime number)

let $p_n$ any prime satisfy the above

for instance $p_5=11$ then $p_5\#=2310$

$11<2310-2213<13*13$

$11<97<169$ it's OK

Then 97 must be a prime.

THE PROOF

$(a)$ and $(p_n\#-a)$ are symmetrical around $\frac {p_n\#}{2}$

Let $a=\frac {p_n\#}{2}+b$ then $(p_n\#-a)=\frac {p_n\#}{2}-b$

$p_n\#=(\frac {p_n\#}{2}+b)+(\frac {p_n\#}{2}-b)$

assume that $(\frac {p_n\#}{2}+b)$ is divisible by $\{p_k : p_k \le p_n\}$

then $(\frac {p_n\#}{2}-b)$ must be divisible by $p_k$ too

because $\frac {p_n\#}{2}$ is always divisible by any prime $2 < p_k \le p_n$ so if $(+b)$ is divisible by $p_k$ then $(-b)$ is divisible as well. and if $(\frac {p_n\#}{2}+b)$ is not divisible by any prime of $\{p_k : p_k \le p_n\}$ then $(\frac {p_n\#}{2}-b)$ should be also not divisible by the same prime. So we have this range which we can define the symmetry of the numbers that are not divisible by $\{p_k : p_k \le p_n\}$. that range is from $(p_n+1)$ to $(p_n\#-(p_n+1))$ then $a$ should always greater than $p_n$ $(a > p_n)$

but unfortunately this range of symmetry is broken by the primes greater than $p_n$ because $p_n\#$ is not divisible by $p_{n+1}$ and greater.

So the limits of symmetry ,which can not be affected by the primes greater than $p_n$ , can be defined between $p_n$ and $p_{n+1}^2$

So if $(p_n\#-a)$ satisfy $p_n \lt p_n\#-a \lt p_{n+1}^2$ then it is in the range of symmetry and if $(a)$ is prime then $(p_n\#-a)$ is also prime

but if $(p_n\#-a)$ is prime then $(a)$ could be prime because it will not be divisible by $\{ p_k : p_k \le p_n\}$ but on the other hand it could be divisible by the primes greater than $p_n$ because it is may located out of the range where the symmetry is broken.


We can notice the symmetry in these extra examples

1) For $p_3\#=2*3*5=30$
$p_{n+1}^2=7∗7=49$
so all the primes $5 < p < 30$ are symmetrical around 15 $\frac {p_n\#}{2}=15$ note that $15±2 , 15±4 , 15±8$ are all primes.

2) For $p_4=210$ $p_{n+1}^2=11∗11=121$, number $121$ is less than $210$ which will break the symmetry starting from $121$ so the range that will maintain the symmetry is $(7 < 210-a < 121)$ , $a > 7$
$\frac {p_n\#}{2}=105$ note that $105±2 , 105±4 , 105±8$ are primes etc...
Let $a=151$ (prime number) then $210-151=59$
$7 < 59 < 121$ then $59$ is a prime.