A new proof of $\left ( \lim_{x\rightarrow 0} {sin(x) \over x} \right )$ by using Euler reflection formula.

Euler reflection formula

$${\pi \over {sin(\pi a)} } = \Gamma (a)\Gamma (1-a)$$

where  $a\notin \mathbb{Z}$ 

let  $x = \pi a \Rightarrow a = {x \over \pi}$

So the formula can be written as:

$$\sin(x) = {\pi \over {\Gamma({x \over \pi}) \Gamma(1 - {x \over \pi})}}$$

where  ${x \over \pi}\notin \mathbb{Z}$

Thus, we have.

$$\lim_{x \rightarrow 0}{\sin(x) \over x} = \lim_{x \rightarrow 0}{1 \over {{x \over \pi}\Gamma({x \over \pi}) \Gamma(1 - {x \over \pi})}}$$

$$= \lim_{x \rightarrow 0}{1 \over {\Gamma({{x \over \pi} + 1}) \Gamma(1 - {x \over \pi})}}$$

$$= {1 \over {\Gamma({0 + 1}) \Gamma(1 - 0)}}  = {1 \over {\Gamma({1})^2}} = 1$$

Theory of infinity [2]

As seen in the picture

Zero is just a point in the world of numbers.
and also world of numbers is just a point in the world of infinity.

This lead us to think out of the box for what is beyond zero and infinity.

Theory of infinity

Soppose that:
$$y=\lim_{n \to +\infty} n$$
then $\frac 1y$ approaches $\frac 1{-y}$ as $n$ goes to $+\infty$
So, we can say that $\frac 1y \to \frac 1{-y}$
 And therefore
 $(y \to -y)$ as $(n \to +\infty)$

From this simple test we realize that there is only one infinity and the so-called $(+\infty , -\infty)$ are just two values approches to each other at one infinity without a sign ( without a sign because it is not a number)

So I can redefine the infinity as three types:
*Infinity: it is not a number therefore it has not a sign and it is equal to $\frac 10$
*Positive infinity: the biggest positive number and it is equal to $\frac 1{0^+}$
*Negative infinity: the smallest negative number and it is equal to $\frac 1{0^-}$

The methodology of this theory is like reimann sphere, but in this theory, I imagine the "numbers line" as very big circle that has diameter approaching to infinity so that its curve is really straight as we normally used to see it graphically.

One would say if $+\infty$ and $-\infty$ approaches to each other at infinity, why they give different values on a simple equation like $y=e^x$

$y=e^{+\infty}=+\infty$
$y=e^{-\infty}=0$

The answer of this question is quite simple.
because the same problem can happen to zero or any other number like this equation.
$y= \frac 1x$ has two different values at $x=0^+$ and $x=0^-$ and I can give many different example of two different limits around one number (left and right side).
So does it means we have two different zeros or numbers, absolutely not.

Logic relations of Monomial symmetric polynomials

You can visit Symmetric polynomial webpage on this link
http://en.wikipedia.org/wiki/Symmetric_polynomial#Monomial_symmetric_polynomials

Monomial symmetric polynomials is nice notation for symmetric polynomials especially when the polynomial becomes so long expression like,

$M_{(1,2)}(a,b,c,d,e)=ab^2+ac^2+ad^2+ae^2+ba^2+bc^2+bd^2+be^2+ca^2+cb^2+cd^2+ce^2+da^2+db^2+dc^2+de^2+ea^2+eb^2+ec^2+ed^2$

In this post I will give nice logic relations of Monomial symmetric polynomials, which can help to solve polynomial equations like cubic and quadric equations.

Now check this logic relations

1) $(a^2+b^2)-(a+b)(a+b)+ab(a^0+b^0)=0$

2) $(a^3+b^3+c^3)-(a+b+c)(a^2+b^2+c^2)+(ab+bc+ca)(a+b+c)-abc(a^0+b^0+c^0)=0$

For the next relation I will use the notation of Monomial symmetric polynomials

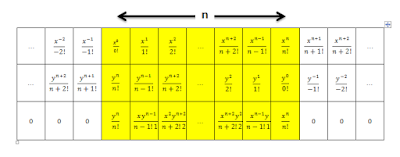
3) $M_{(4)}(a,b,c,d) - M_{(1)}(a,b,c,d) \cdot M_{(3)}(a,b,c,d) + M_{(1,1)}(a,b,c,d) \cdot M_{(2)}(a,b,c,d) - M_{(1,1,1)}(a,b,c,d) \cdot M_{(1)}(a,b,c,d)  + M_{(1,1,1,1)}(a,b,c,d) \cdot M_{(0)}(a,b,c,d)=0$

And for more general form for 4 variables $(a,b,c,d)$ we have,

$M_{(n)}(a,b,c,d) - M_{(m)}(a,b,c,d) \cdot M_{(n-m)}(a,b,c,d) + M_{(m,m)}(a,b,c,d) \cdot M_{(n-2m)}(a,b,c,d) - M_{(m,m,m)}(a,b,c,d) \cdot M_{(n-3m)}(a,b,c,d)  + M_{(m,m,m,m)}(a,b,c,d) \cdot M_{(n-4m)}(a,b,c,d) =0$
for $(n = 4m)$
Or
$M_{(n)}(a,b,c,d) - M_{(m)}(a,b,c,d) \cdot M_{(n-m)}(a,b,c,d) + M_{(m,m)}(a,b,c,d) \cdot M_{(n-2m)}(a,b,c,d) - M_{(m,m,m)}(a,b,c,d) \cdot M_{(n-3m)}(a,b,c,d)  + M_{(n-3m,m,m,m)}(a,b,c,d) =0$
for $(n \gt 4m)$

If we want to generalize the formula for unknown number of variables $(a_1,a_2, \cdots , a_n)$
We should have new definition of extended Monomial symmetric polynomials.

Let us define $M_{(k)}^{(n)}(a_1,a_2,\cdots , a_n)$ as a Monomial symmetric polynomials that has $n$ number of $k$ powers for the given variables.

So I can say:
$$M_{(k)}^{(n)}(a_1,a_2,\cdots , a_n)=M_{(k,k, … k)}(a_1,a_2, \cdots , a_n)$$ $k$ is repeated $n$ times.


The new definition will help us to construct  a formula  to generalize a relation for unknown number of variables $(a_1,a_2, \cdots , a_n)$

So we have,
$$\sum_{m=0}^{n}\left( (M_{(n-m)}^{(j)}(a_1,a_2, \cdots , a_n))\cdot \sum_{1}^{n} a_k^{jm}\right)=0$$
$j \in \Bbb N$

Unified method to find formula for polynomial equation roots.

Here is unified solution routine to find formula for any $nth$ degree equation ,  for $n < 5$
We can write The general form for any polynomial equation of any $nth$ degree as:
$$\sum_{j=0}^{n} a_j x^j =a_0+a_1x+a_2x^2+\cdots + a_nx^n =0$$
where $a_n \neq 0$

After dividing the equation by $a_n$ , the substitution $x=y-\frac{a_{n-1}}{na_n}$ will eliminate the term $a_{n-1}x^{n-1}$ so we have,
$$\sum_{j=0}^{n}\left(b_jy^j\right) -b_{n-1}y^{n-1}=b_0+b_1y+b_2y^2+\cdots+b_{n-2}y^{n-2}+b_ny^n$$
As we know that the quadratic equation is already solved by this substitution , but remain the cubic and the quartic which will be solved in the following steps:

For the cubic equation, I will rewrite it  as,
$$y^3+py+q=0 \tag1$$
Let $y=z_1+z_2$
$y^3=z_1^3+3z_1^2z_2+3z_1z_2^2+z_2^3=z_1^3+3z_1z_2(z_1+z_2)+z_2^3$
$$y^3-3z_1z_2x-(z_1^3+z_2^3)=0 \tag 2$$

By comparing the coefficients of $eq(2)$ with the original equation (1) we get,
$p=-3z_1z_2 \Rightarrow z_1^3z_2^3=\frac{-p^3}{27}$
and
 $q=-(z_1^3+z_2^3)$
assume that $z_1^3$ and $z_2^3$ are roots of $z^3$ then we can write the equation as,
$$(z^3-z_1^3)(z^3-z_2^3)=0$$
and by expanding the equation we have,
$$z^6-(z_1^3+z_2^3)z^3+z_1^3z_2^3=0$$
So we finally have,
$$z^6+qz^3-\frac{p^3}{27}=0$$
$z_1=\sqrt[3]{-\frac q2+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$
$z_2=\sqrt[3]{-\frac q2-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$
$$\begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ \end{bmatrix}=\begin{bmatrix} z_1 \\ z_2 \\ \end{bmatrix} * \begin{bmatrix} 1 & 1 \\ \omega & \omega^2 \\ \omega^2 & \omega \\ \end{bmatrix}$$
$\omega$ is imaginary cubic root of unity.
$x_j=y_j-\frac{a_2}{3a_3} , j=1,2,3$

For the quartic equation, I will rewrite it as,
$$y^4+py^2+qy+r=0 \tag 3$$
Let $y=z_1+z_2+z_3$
By squaring both sides
$y^2=z_1^2+z_2^2+z_3^2+2(z_1 z_2+z_1 z_3+z_2 z_3)$
$y^2-(z_1^2+z_2^2+z_3^2)=2(z_1 z_2+z_1 z_3+z_2 z_3)$
By squaring both sides again.
$y^4-2(z_1^2+z_2^2+z_3^2 ) y^2+(z_1^2+z_2^2+z_3^2 )^2=4(z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2+2(z_1^2 z_2 z_3+z_1 z_2^2 z_3+z_1 z_2 z_3^2 ))$

$y^4-2(z_1^2+z_2^2+z_3^2 ) y^2+(z_1^2+z_2^2+z_3^2 )^2=4(z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2)+8z_1 z_2 z_3 (z_1+z_2+z_3 )$

$$y^4-2(z_1^2+z_2^2+z_3^2 ) y^2-8(z_1 z_2 z_3)y+(z_1^2+z_2^2+z_3^2 )^2-4(z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2 )=0 \tag 4$$

By comparing the coefficients of $eq(4)$ with the original equation (3) we get,
$p=-2(z_1^2+z_2^2+z_3^2 )$
$q=-8(z_1 z_2 z_3 )$
$r=(z_1^2+z_2^2+z_3^2 )^2-4(z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2 )$
and by some little steps of substitution we get,
$z_1^2+z_2^2+z_3^2 =-\frac p2$
$z_1^2 z_2^2 z_3^2=\frac {q^2}{64}$
$z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2=\frac{p^2-4r}{16}$
assume that $z_1^2$ , $z_2^2$ and $z_3^2$ are roots of $z^2$ then we can write the equation as,
$$(z^2-z_1^2)(z^2-z_2^2)(z^2-z_3^2)=0$$
and by expanding the equation we have,
$$z^6-(z_1^2+z_2^2+z_3^2 ) z^4+(z_1^2 z_2^2+z_1^2 z_3^2+z_2^2 z_3^2 ) z^2-z_1^2 z_2^2 z_3^2=0$$
By substitution we get a cubic equation,
$$z^6+\frac p2 z^4+\left(\frac{p^2-4r}{16}\right) z^2-\frac{q^2}{64}=0$$
So we finally have,
$$\begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ \end{bmatrix}=\begin{bmatrix} z_1 \\ z_2 \\ z_3 \\ \end{bmatrix} * \begin{bmatrix} 1 & 1 & 1 \\ 1 & -1 & -1 \\ -1 & 1 & -1 \\  -1 & -1& 1 \\ \end{bmatrix}$$
$x_j=y_j-\frac{a_3}{4a_4} , j= 1,2,3,4$

For higher degree equations,

There is no formula for higher degree equations in radicals
Abel–Ruffini theorem  and Galois theory have proved the impossibility of solving quintic  and higher degree equations in radicals.

A study on half-order differentiation of exponential function

Before you read this topic I advise you to read the following posts first.

The Binomial Theorem proof by exponentials

Fractional Calculus of Zero

Disproving D^{1/2}e^x=e^x with explanation

The following picture is showing graphically the relation between $e^x$ expansion terms and Reciprocal gamma function.
The plot is for $x=1,x=2,x=3$
Also it shows the differentiation and integration manner of $e^x$.

Click on the image to enlarge it

So if we move the terms of $e^x$ half step to the direction of differentiation, we will get the terms of half-integers order differentiation.
$$D_x^{1/2}(e^x)=\cdots +\frac{x^{-3/2}}{(-3/2)!}+\frac{x^{-1/2}}{(-1/2)!}+\frac{x^{1/2}}{(1/2)!}+\frac{x^{3/2}}{(3/2)!}+\cdots$$
(Note that when I use non-integer factorials (a)! I am indeed referring to Gamma function)
Now the question which I am trying to answer is:
 "Does this series converges? and how to deal with it in case of it diverges?"

I will use $e_{\alpha}^x$ as annotation for $D_x^{\alpha}(e^x)$
I recently proved this nice relation where $a,b \in \Bbb R$
$$e^a\cdot e_{\alpha}^b=e_{\alpha}^{a+b} \tag1$$
Which I can prove it by using the binomial formula from the previous post
$$\frac{(a+b)^{\alpha}}{\alpha!}=\sum_{k \in \Bbb Z} \frac{a^k}{k!} \cdot \frac{b^{\alpha-k}}{(\alpha-k)!}$$
And I already proved ,in the previous post, that the binomial theorem is actually a term of two multiplied exponential function ($\alpha$ can be any real number).

By using $eq(1)$ let us now test the relation for $\alpha=\frac12$
For $a=0$ we have,
$e^0\cdot e_{1/2}^b=e_{1/2}^{0+b} \Rightarrow e_{1/2}^b=e_{1/2}^b$
and that is a logical result.

For $b=0$ we have,
$e^a\cdot e_{1/2}^0=e_{1/2}^{a+0} \Rightarrow e^a \cdot e_{1/2}^0=e_{1/2}^a$
We all know that $e_{1/2}^0=\infty$
Hence $$e_{1/2}^a=\infty \cdot e^a$$

Therefore the expansion series of $e_{1/2}^a$ is not well-defined, but actually if we look to fractional calculus of 'zero number' which I studied it before in an earlier post makes the whole fractional calculus undefined and for that reason we always set the zero fractional calculus value to zero.

Thus we always have to eliminate the expansion series terms of $e_{1/2}^a$  that met the half-order differentiation of zero expansion so that it finally converges.
$$D_x^{1/2}(e^x)=\frac{x^{-1/2}}{(-1/2)!}+\frac{x^{1/2}}{(1/2)!}+\frac{x^{3/2}}{(3/2)!}+\frac{x^{5/2}}{(5/2)!}+\cdots$$

The Binomial Theorem proof by exponentials.

The famous furmula for the binomial is
$$(a+b)^n=\sum_{k=0}^{\infty} \binom nk a^k b^{n-k}$$
But we can also express the formula like this
$${(a+b)^n \over n!}=\sum_{k \in \Bbb Z} \frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!}$$
Actually the binomial structure is coming from the $nth$ term when multiplying two exponentials together , see the following picture.

Click on the image to enlarge it

The first row of the table is $e^x$ terms, the second row is $e^y$ terms arranged backwards and the last row is the result of multiplying every term from the first row by the opposite term in the second row.

The distance $n$ is from the zero term of the first row $e^x$ to the zero term of the second row $e^y$

So we can prove the binomial theorem by the following steps:
$$e^{a+b}=e^a e^b \tag1$$
$$\sum_{n \in \Bbb Z} \frac {(a+b)^n}{n!}=\left(\sum_{n \in \Bbb Z} \frac {a^n}{n!} \right) \left( \sum_{n \in \Bbb Z} \frac {b^n}{n!}\right) \tag2$$
We can use "Cauchy product of two infinite series" to multiply the two series in RHS in $eq(2)$.
$$\left(\sum_{n \in \Bbb Z} \frac {a^n}{n!} \right) \left( \sum_{n \in \Bbb Z} \frac {b^n}{n!}\right)=\sum_{n \in \Bbb Z}\left( \sum_{k \in \Bbb Z}\frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!} \right) \tag3$$
From $eq(2)$ & $eq(3)$ we get:
$$\sum_{n \in \Bbb Z} \frac {(a+b)^n}{n!}=\sum_{n \in \Bbb Z}\left( \sum_{k \in \Bbb Z}\frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!} \right) \tag4$$
Now it is clearly that every term of the series in the LHS is equal to the same $nth$ term in the RHS.

So we finally have
$${(a+b)^n \over n!}=\sum_{k \in \Bbb Z} \frac {a^k}{k!} \frac {b^{n-k}}{(n-k)!} \tag5$$
Which indeed the same known binomial formula:
$$(a+b)^n=\sum_{k=0}^{\infty} \binom nk a^k b^{n-k}$$